P4251 [SCOI2015]小凸玩矩阵

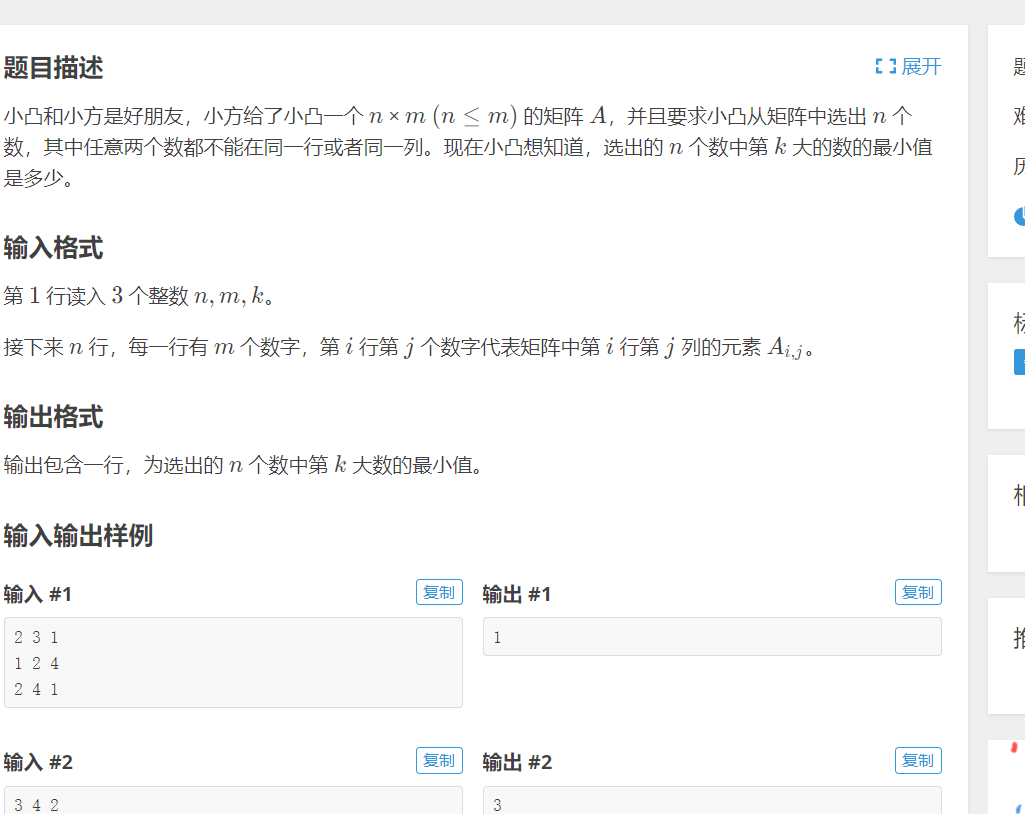
 题解：求第K大，要求第K大最小，一般都是二分答案

然后不是同一行同一列，显然又是匹配问题

考虑<=x的值，要大于等于n-k+1

然后不断找最小答案，

每次判断答案把图给clear掉，然后重新建图就行了

建模的问题的话，考虑是行和列作为点，然后点作为边，这样考虑就行了，把小于x的元素建边就行了 ，

因为他最多选min（n,m）个点，所以每个行和列只能用一次

#include<bits/stdc++.h>
using namespace std;
const int inf=1e9+5;
const int maxn=505;
struct edg
{
    int to,cap,rev;
   edg() :to(), cap(), rev(){}
  edg(int a, int  b, int  c) :to(a), cap(b), rev(c){}

};
vector<edg> G[maxn];
int iter[maxn];
int level[maxn];
void add(int from,int to,int cap)
{
    G[from].push_back(edg(to,cap,G[to].size()));
    G[to].push_back(edg(from,0,G[from].size()-1));
}
void bfs(int s)
{
    memset(level,-1,sizeof(level));
    queue<int> que;
    level[s]=0;
    que.push(s);
    while(que.size()>0)
    {
        int v=que.front();
        que.pop();
        for(int i=0;i<G[v].size();i++)
        {
            edg &e=G[v][i];
            if(e.cap>0&&level[e.to]<0)
            {
                level[e.to]=level[v]+1;
                que.push(e.to);
            }
        }
    }
}
int dfs(int v,int t,int f)
{
    if(v==t)
         return f;
    for(int &i=iter[v];i<G[v].size();i++)
    {
        edg &e=G[v][i];
        if(e.cap>0&&level[v]<level[e.to])
        {
            int d=dfs(e.to,t,min(f,e.cap));
            if(d>0)
            {
                e.cap-=d;
                G[e.to][e.rev].cap+=d;
                return d;
            }
        }
    }
    return 0;
}
int _maxflow(int s,int t)
{
    int flow=0;
    for( ; ;)
    {
        bfs(s);
        if(level[t]<0)return flow;
        memset(iter,0,sizeof(iter));
        int f;
        while((f=dfs(s,t,inf))>0)
        {
            flow+=f;
        }
    }
}
int n,m,k;
int a[251][251];
int ans[90000];
int tail=1;
bool check(int mid)
{   for(int i=0;i<=n+m+1;i++)
      G[i].clear();
    int x=ans[mid];
    for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++)
    if(a[i][j]<=x) add(i,j+n,1);
    for(int i=1;i<=n;i++)
    {
         add(0,i,1);
    }
    for(int i=1;i<=m;i++)
    {
       add(n+i,n+m+1,1);
    }
    return _maxflow(0,m+n+1)>=n-k+1;
}
int main()
{
   cin>>n>>m>>k;
   for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++) {
            cin>>a[i][j];
            ans[tail++]=a[i][j];
    }
   int l=1,r=tail-1;
   int anss;
   sort(ans+1,ans+tail);
   while(l<=r)
   {
       int mid=l+r>>1;
       if(check(mid))
       {
           anss=ans[mid];
           r=mid-1;
       }
       else l=mid+1;

   }
   cout<<anss<<endl;




}