题目描述
如题,给出一个网络图,以及其源点和汇点,求出其网络最大流。
输入格式
第一行包含四个正整数N、M、S、T,分别表示点的个数、有向边的个数、源点序号、汇点序号。
接下来M行每行包含三个正整数ui、vi、wi,表示第i条有向边从ui出发,到达vi,边权为wi(即该边最大流量为wi)
输出格式
一行,包含一个正整数,即为该网络的最大流。
输入输出样例
输入 #1 复制
4 5 4 3
4 2 30
4 3 20
2 3 20
2 1 30
1 3 40
输出 #1 复制
50
说明/提示
时空限制:1000ms,128M
数据规模:
对于30%的数据:N<=10,M<=25
对于70%的数据:N<=200,M<=1000
对于100%的数据:N<=10000,M<=100000
样例说明:
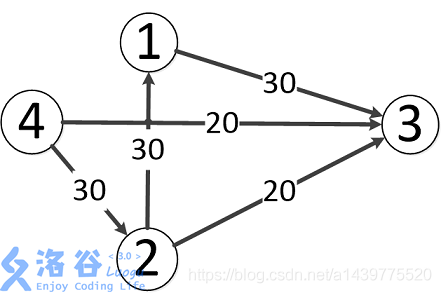
题目中存在3条路径:
4-->2-->3,该路线可通过20的流量
4-->3,可通过20的流量
4-->2-->1-->3,可通过10的流量(边4-->2之前已经耗费了20的流量)
故流量总计20+20+10=50。输出50。
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
import java.util.StringTokenizer;
public class Main {
public static class node{ //存边
private int to;
private int next;
private int v;
public node(){
}
}
public static class pre{ //记录路径
private int e; //该边的编号
private int b; //该边的去向
public pre(){
}
public pre(int b,int e){
this.b=b;
this.e=e;
}
}
static int cnt=0,head[];
static node a[];
static pre pre[];
static boolean vis[];
static int n,m,s,t;
public static void main(String[] args) {
FastScanner fs = new FastScanner();
n=fs.nextInt(); //源点总数
m=fs.nextInt(); //边的数量
s =fs.nextInt(); //起点
t=fs.nextInt(); //终点
a=new node[2*(m+1)];
head=new int[n+1];
for (int i = 0; i <=n; i++) {
head[i]=-1;
}
for (int i = 0; i <m; i++) { //存数据
int x=fs.nextInt();
int y=fs.nextInt();
int v=fs.nextInt();
add(x,y,v);
add(y,x,0);
}
System.out.println(ek());
}
public static void add(int x,int y,int v){ //前向星存
a[cnt]=new node();
a[cnt].to=y;
a[cnt].v=v;
a[cnt].next=head[x];
head[x]=cnt++;
}
public static boolean bfs(){ //寻找是否有增广路
vis=new boolean[n+1]; //标记访问,防止重复访问
pre=new pre[n+1]; //初始化记录路径
Queue<Integer> d=new LinkedList();
vis[s]=true;
d.offer(s);
while(!d.isEmpty()){
int v=d.poll();
for(int u=head[v];;u=a[u].next){ //搜寻该点所有的边
if(u==-1)break; //到头了就结束
int f=a[u].to;
if(!vis[f]&&a[u].v>0){ //查看是否访问和是否为可行流
vis[f]=true;
pre[f]=new pre(v,u); //标记路径,后面好更新
if(f==t)return true;
d.offer(f);
}
}
}
return false;
}
public static int ek(){
int ans=0;
while(bfs()){
int min=Integer.MAX_VALUE;
for (int i =t; i!=s; i=pre[i].b) { //寻找这条路可流入量
min=Math.min(min,a[pre[i].e].v);
}
for (int i =t; i!=s; i=pre[i].b) { //更新
if(pre[i].e%2!=0){ //该边减,对应的相反边加
a[pre[i].e].v-=min;
a[pre[i].e-1].v+=min;
}else{
a[pre[i].e].v-=min;
a[pre[i].e+1].v+=min;
}
}
ans+=min; //流入量
}
return ans;
}
public static class FastScanner {
private BufferedReader br;
private StringTokenizer st;
public FastScanner() {
br = new BufferedReader(new InputStreamReader(System.in));
}
public String nextToken() {
while(st == null || !st.hasMoreElements()) {
try {
st = new StringTokenizer(br.readLine());
} catch (IOException e) {
// TODO Auto-generated catch block
e.printStackTrace();
}
}
return st.nextToken();
}
public int nextInt() {
return Integer.valueOf(nextToken());
}
}