树状数组[数据结构]

树状数组

——!x^n+y^n=z^n

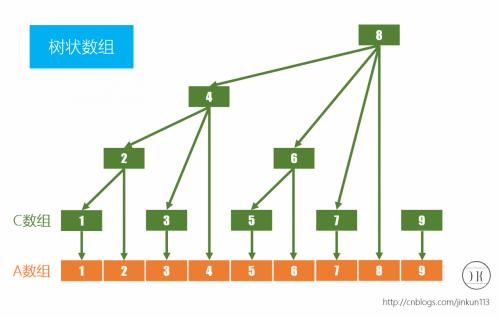
　　额，图是网上搜来的...

　　如图：

我们令

c[1]=a[1]

c[2]=a[2]+c[1]

c[3]=a[3]

c[4]=a[4]+c[3]+c[2]

c[5]=a[5]

c[6]=c[5]+a[6]

c[7]=a[7]

c[8]=a[8]+c[4]+c[6]+c[7]

c[9]=a[9]

　　其实我们是令c[n]的管辖范围为i个元素，而这个i为n化为二进制时从后往前第一个出现1的地方及后面的0组成数的大小（记为lowbit（n））。

　　举个例子c[6]=a[5]+a[6]

6=（110）₂，lowbit（6）=（10）₂=2；

　　但这会产生一个问题，怎么求lowbit？

　　利用计算机补码特性我们可以得到：

lowbit（x）=x&（-x）。[知道补码的同学手推即可，不知道赶紧百度]

　　当然作为数据结构要有他的用处。

　　利用树状数组我们可以进行两个比较简单的操作：

<i>求a[1]+a[2]+L+a[x]的值

<ii>单点更新

---

<i>区间查询

假设我们要求1~x的区间和，我们可以先查询c[x]，显然c[x]是包含于我们要求的范围里的；

但当我们查询完c[x]后，我们应该继续查询未查询到的部分；

注意到：c[x]的管辖范围：[x-lowbit（x）+1,x]，故我们应继续查询c[x-lowbit（x）]；

反复上面操作直至查询完毕。

代码：

int getsum(x){
    int res=0;
    for(;x;x-=lowbit(x))
        res+=bit[x];
    return res;
}

　　本人树状数组一直喜欢打成bit啊...

<ii>单点更新

我们希望a[x]+inc

当然我们会先让c[x]+inc；

然后我们需要找到管辖c[x]的c[y]，因为x必须∈[y-lowbit（y）+1,y]，我们怎么做这件事？

其实我们只需要在x后面补上一个0就行了，想想是不是这样。

代码：

void update(x,inc){
    for(;x<=n;x+=lowbit(x))
        bit[x]+=inc;
}

　　怎么样，是不是觉得代码简短很多？（对比线段树）