【qbxt！预习】二叉堆

qxbt的老师发消息来说让自己预习，本来想中考完之后认真学（颓）习（废）  没办法

0. 数据结构图文解析系列

 

1. 二叉堆的定义

二叉堆是一种特殊的堆，二叉堆是完全二叉树或近似完全二叉树。二叉堆满足堆特性：父节点的键值总是保持固定的序关系于任何一个子节点的键值，且每个节点的左子树和右子树都是一个二叉堆。
当父节点的键值总是大于或等于任何一个子节点的键值时为最大堆。 当父节点的键值总是小于或等于任何一个子节点的键值时为最小堆。

2. 二叉堆的存储

二叉堆一般使用数组来表示。请回忆一下二叉树的性质，其中有一条性质：

性质五：如果对一棵有n个节点的完全二叉树的节点按层序编号（从第一层开始到最下一层，每一层从左到右编号，从1开始编号），对任一节点i有：

1. 如果i=1 ，则节点为根节点，没有双亲。
2. 如果2 * i > n ，则节点i没有左孩子 ；否则其左孩子节点为2*i . （n为节点总数）
3. 如果2 * i+1>n ，则节点i没有右孩子；否则其右孩子节点为2*1+1.

简单来说：

1. 如果根节点在数组中的位置是1，第n个位置的子节点分别在2n 与 2n+1，第n个位置的双亲节点分别在⌊i /2⌋。因此，第1个位置的子节点在2和3.
2. 如果根节点在数组中的位置是0，第n个位置的子节点分别在2n+1与2n+2，第n个位置的双亲节点分别在⌊（i-1） /2⌋。因此，第0个位置的子节点在1和2.

得益于数组的随机存储能力，我们能够很快确定堆中节点的父节点与子节点。

下面以大顶堆展示一下堆的数组存储。

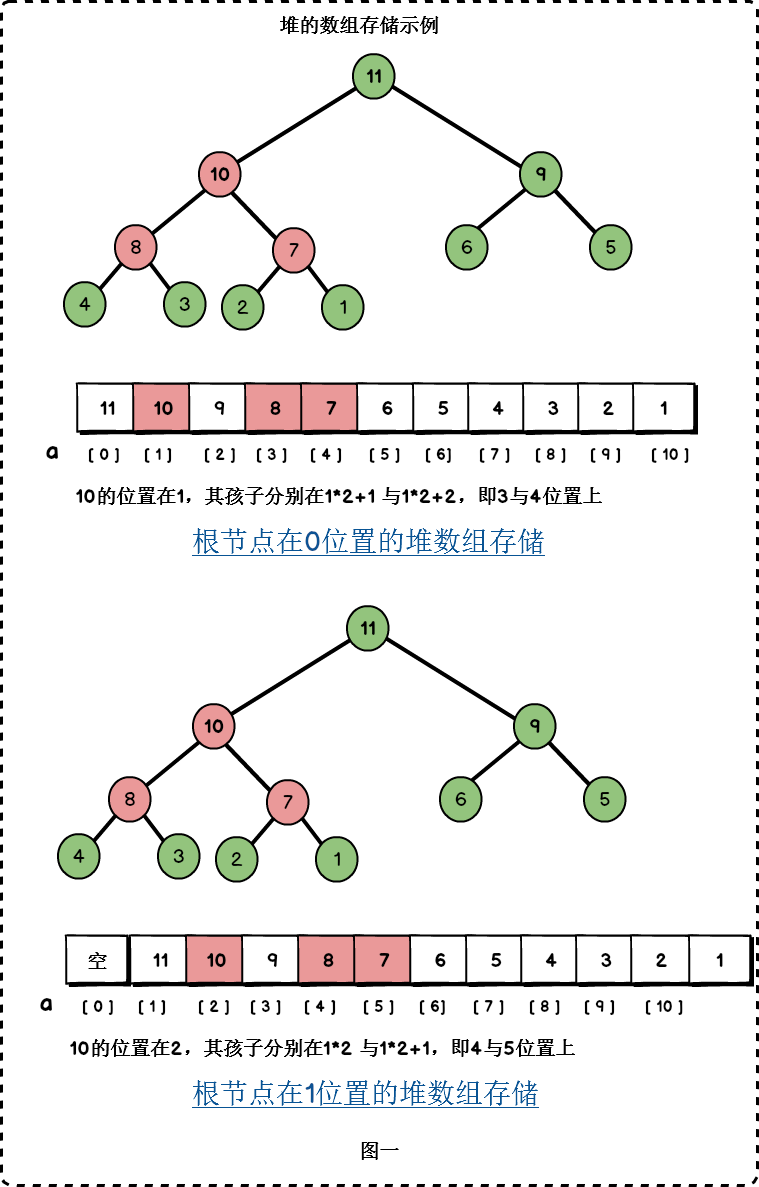
在本文中，我们以大顶堆为例进行堆的讲解。本文大顶堆的根节点位置为0.

3. 二叉堆的具体实现

在二叉堆上可以进行插入节点、删除节点、取出堆顶元素等操作。

3.1 二叉堆的抽象数据类型

/*大顶堆类定义*/
template <typename T>
class MaxHeap
{
public:
    bool insert(T val);     //往二叉堆中插入元素
    bool remove(T data);    //移除元素
    void print();           //打印堆
    T getTop();             //获取堆顶元素
    bool createMaxHeap(T a[], int size);//根据指定的数组来创建一个最大堆

    MaxHeap(int cap = 10);
    ~MaxHeap();

private:
    int capacity;   //容量，也即是数组的大小
    int size;       //堆大小，也即是数组中有效元素的个数
    T * heap;       //底层的数组
private:
    void filterUp(int index); //从index所在节点，往根节点调整堆
    void filterDown(int begin ,int end ); //从begin所在节点开始，向end方向调整堆
};

1. 注意capacity与size的区别。capacity指的是数组的固有大小。size值数组中有效元素的个数，有效元素为组成堆的元素。
2. heap为数组。

3.2 二叉堆的插入

在数组的最末尾插入新节点，然后自下而上地调整子节点与父节点的位置：比较当前结点与父节点的大小，若不满足大顶堆的性质，则交换两节点，从而使当前子树满足二叉堆的性质。时间复杂度为O(logn)。
当我们在上图的堆中插入元素12：

调整过程：

1. 节点12添加在数组尾部，位置为11；
2. 节点12的双亲位置为⌊11/2⌋ = 5，即节点6；节点12比节点6大，与节点6交换位置。交换后节点12的位置为5.
3. 节点12的双亲位置为⌊ 5 /2⌋ = 2,即节点9；节点12比节点9大，与节点9交换位置。交换后节点12的位置为2.
4. 节点12的双亲位置为⌊2/2⌋ = 1，即节点11；节点12比节点11大，与节点11交换位置。交换后节点12的位置为1.
5. 12已经到达根节点，调整过程结束。

   /*从下到上调整堆*/
   /*插入元素时候使用*/
   template <typename T>
   void MaxHeap<T>::filterUp(int index)
   {
       T value = heap[index];  //插入节点的值，图中的12
   
       while (index > 0) //如果还未到达根节点，继续调整
       {
           int indexParent = (index -1)/ 2;  //求其双亲节点
           if (value< heap[indexParent])
               break;
           else 
           {
               heap[index] = heap[indexParent];
               index = indexParent;
           }
       }
       heap[index] = value;    //12插入最后的位置
   };

   在真正编程的时候，为了效率我们不必进行节点的交换，直接用父节点的值覆盖子节点。最后把新节点插入它最后的位置即可。

   基于这个调整函数，我们的插入函数为：

   /*插入元素*/
   template <typename T>
   bool MaxHeap<T>::insert(T val)
   {
       if (size == capacity) //如果数组已满，则返回false
           return false;
       heap[size] = val;
       filterUp(size);
       size++;
       return true;
   };

   3.3 二叉堆的删除

   堆的删除是这样一个过程：用数组最末尾节点覆盖被删节点，再从该节点从上到下调整二叉堆。我们删除根节点12：
   

   可能有人疑惑，删除后数组最末尾不是多了一个6吗？
   的确，但我们把数组中有效元素的个数减少了一，最末尾的6并不是堆的组成元素。

   这个从上到下的调整过程为：

   /*从上到下调整堆*/
   /*删除元素时候使用*/
   template<typename T>
   void MaxHeap<T>::filterDown(int current,int end)
   {
   
       int child = current * 2 + 1; //当前结点的左孩子
   
       T value = heap[current];    //保存当前结点的值
   
       while (child <= end)
       {
           if (child < end && heap[child] < heap[child+1])//选出两个孩子中较大的孩子
               child++;
           if (value>heap[child])  //无须调整；调整结束
               break;
           else
           {
               heap[current] = heap[child];    //孩子节点覆盖当前结点
               current = child;                //向下移动
               child = child * 2 + 1;          
           }
       }
       heap[current] = value;
   };

   基于调整函数的删除函数：

   /*删除元素*/
   template<typename T>
   bool MaxHeap<T>::remove(T data)
   {
       if (size == 0) //如果堆是空的
           return false;
       int index;
       for (index = 0; index < size; index++)  //获取值在数组中的索引
       {
           if (heap[index] == data)
               break;
       }
       if (index == size)            //数组中没有该值
           return false; 
    
       heap[index] = heap[size - 1]; //使用最后一个节点来代替当前结点，然后再向下调整当前结点。
    
       filterDown(index,size--);  
    
       return true;
   };

   3.4 其余操作

   其余操作很简单，不在这里啰嗦。

   /*打印大顶堆*/
   template <typename T>
   void MaxHeap<T>::print()
   {
       for (int i = 0; i < size; i++)
           cout << heap[i] << " ";
   };
   /*获取堆顶元素*/
   template <typename T>
   T MaxHeap<T>::getTop()
   {
       if (size != 0)
           return heap[0];
   };
   
   /*根据指定的数组来创建一个最大堆*/
   template<typename T>
   bool MaxHeap<T>::createMapHeap(T a[], int size)
   {
       if (size > capacity)    //  堆的容量不足以创建
           return false;
       for (int i = 0; i < size; i++)
       {
           insert(a[i]);
       }
       return true;
   };

   4. 二叉堆代码测试

 

int _tmain(int argc, _TCHAR* argv[])
{
    MaxHeap<int> heap(11);
    //逐个元素构建大顶堆
    for (int i = 0; i < 10; i++)
    {
        heap.insert(i);
    }
    heap.print();
    cout << endl;
    heap.remove(8);
    heap.print();
    cout << endl;

    //根据指定的数组创建大顶堆
    MaxHeap<int> heap2(11);
    int a[10] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
    heap2.createMaxHeap(a, 10);
    heap2.print();
    getchar();
    return 0;
}

输出结果：

9 8 5 6 7 1 4 0 3 2
9 7 5 6 2 1 4 0 3
10 9 6 7 8 2 5 1 4 3