题目链接:https://leetcode-cn.com/problems/delete-node-in-a-bst/
题目描述:
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
首先找到需要删除的节点;
如果找到了,删除它。
说明: 要求算法时间复杂度为 O(h),h 为树的高度。

题解:
有以下五种情况:
第一种情况:没找到删除的节点,遍历到空节点直接返回了
找到删除的节点
第二种情况:左右孩子都为空(叶子节点),直接删除节点, 返回NULL为根节点
第三种情况:删除节点的左孩子为空,右孩子不为空,删除节点,右孩子补位,返回右孩子为根节点
第四种情况:删除节点的右孩子为空,左孩子不为空,删除节点,左孩子补位,返回左孩子为根节点
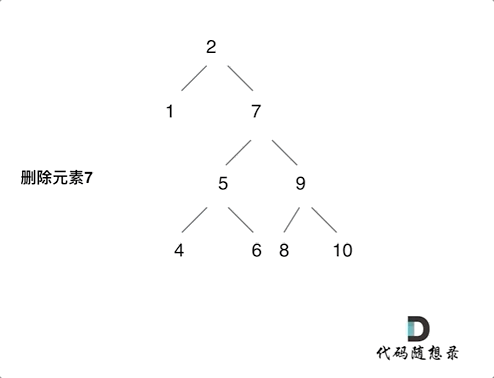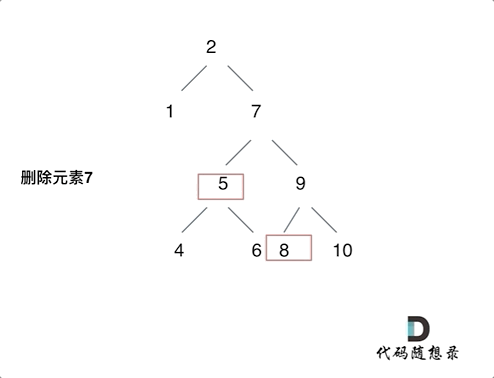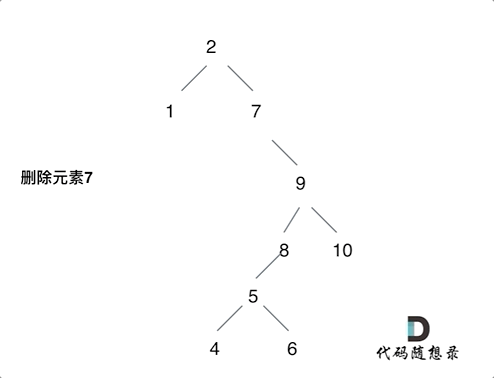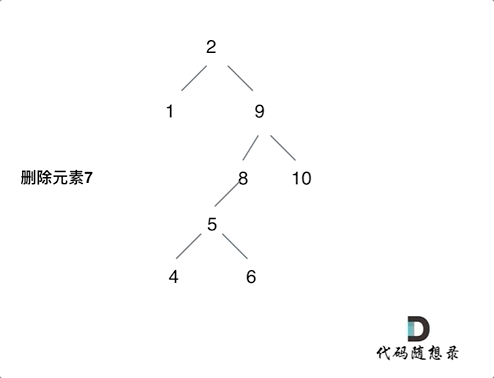
第五种情况:左右孩子节点都不为空,则将删除节点的左子树头结点(左孩子)放到删除节点的右子树的最左面节点的左孩子上,返回删除节点右孩子为新的根节点
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
//第一种情况,没有找到删除的节点
if(root == nullptr) return root;
if(root->val == key)
{ //第二种情况,找到删除的节点,且节点左右节点为空
if(root->left == nullptr && root-> right == nullptr)
return nullptr;
//第三种情况,找到删除的节点,且节点左孩子为空,右节点不为空
if(root->left == nullptr)
return root->right;
//第四种情况,找到删除的节点,且节点右孩子为空,左孩子不为空
else if(root->right == nullptr)
return root->left;
//第五种情况,找到删除的节点,且左右孩子均不空
else
{
TreeNode *cur = root->right; //删除节点右子树的最左边节点
while(cur->left != nullptr)
{
cur = cur->left;
}
cur->left = root->left; //删除节点的左子树节点放到删除节点的右子树的最左节点的左孩子上
TreeNode *node = root;
root = node->right; //删除节点的右孩子作为新的根节点
delete node; //删除节点
return root;
}
}
if(root->val < key) //当前的值小于目标值,
root->right = deleteNode(root->right, key);
if(root->val > key)
root->left = deleteNode(root->left, key);
return root;
}
};