题目链接:https://leetcode-cn.com/problems/longest-common-subsequence
题目描述:
给定两个字符串 text1 和 text2,返回这两个字符串的最长公共子序列的长度。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。
若这两个字符串没有公共子序列,则返回 0。
示例 1:
输入:text1 = "abcde", text2 = "ace"
输出:3
解释:最长公共子序列是 "ace",它的长度为 3。
示例 2:
输入:text1 = "abc", text2 = "abc"
输出:3
解释:最长公共子序列是 "abc",它的长度为 3。
示例 3:
输入:text1 = "abc", text2 = "def"
输出:0
解释:两个字符串没有公共子序列,返回 0。
提示:
1 <= text1.length <= 1000
1 <= text2.length <= 1000
输入的字符串只含有小写英文字符。
解题思路:
1.定义dp数组
一般对于在两个字符串,或者是能拆解成两个字符串的问题当中,我们都定义一个二维dp数组。
dp[i][j]:表示在字符串s[0...i]中和字符串s[0...j]中最长公共子序列的长度为dp[i][j]

2.确定base case:s1或者s2为空串时,即dp[0][j]和dp[i][0]初始为0
3.确定【选择】:s1[i]、s2[j]的值
4.确定【状态】:dp[i][j]的值
5.确定【状态转移方程】
具体到每个字符串的每一个字符,只看s1[i]和s2[j],思考每个字符该做什么能找出公共字符。

如果s1[i] == s2[j],说明这个字符一定在lcs中,所以可以推出dp[i][j] = dp[i-1][j-1]+1;
如果s1[i] != s2[j],说明s1[i]和s2[j]中至少有一个字符不在lcs中,有以下三种情况:
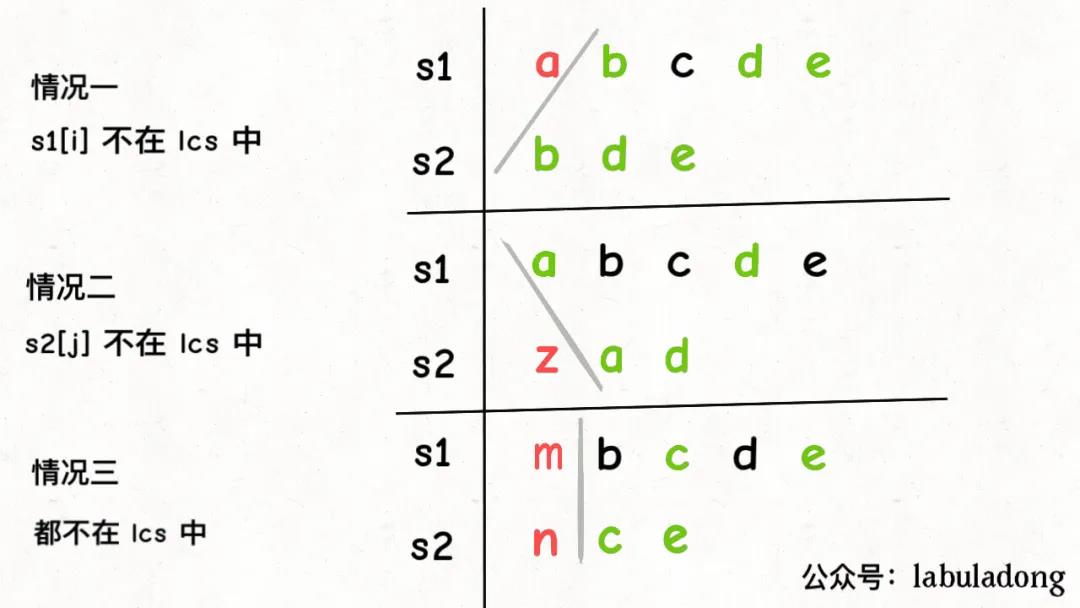
其中,情况三被情况一和情况二包含,由于求最长公共子序列,找出两者中的最大值即可。
代码:
套入动态规划模板即可得出:
class Solution {
public:
int longestCommonSubsequence(string s1, string s2) {
int m = s1.length();
int n = s2.length();
int i,j;
//vector<vector<int>> dp(m+1, vector<int>(n+1, 0));
int dp[m+1][n+1];
for(i = 0; i< m+1; i++)
{
for(j = 0; j < n+1; j++)
{
dp[i][j] = 0;
}
}
// base case
if(s1.length() == 0 || s2.length() == 0) return 0;
for(i = 1; i <= m; i++)
{
for(j = 1; j <= n; j++)
{
if(s1[i-1] == s2[j-1])
{
dp[i][j] = dp[i-1][j-1] + 1;
}else
{
dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
}
}
}
return dp[m][n];
}
};