AcWing 240. 食物链

原题链接：AcWing 240. 食物链

扩展域与边带权的并查集：

并查集实际上是由若干颗树构成的森林，我们可而一再数中的每条边上记录一个权值，即维护一个(d)，用(d[x])保存节点(x)到父节点(fa[x])之间的边权。每次路径压缩之后，每个访问过的节点都会直接指向树根，然后同时更新这些节点的(d)值，就可以利用路径压缩过程来统计每个节点到树根之间的路径上的信息。

代码：

int find(int x) {
	if (p[x] != x) {
		int t = find(p[x]);
		d[x] += d[p[x]];
		p[x] = t;
	}
	
	return p[x];
}

就题论题，这道题不像是一个食物链倒是像一个食物环，(A)吃(B)，(B)吃(C)，(C)吃(A)。
使用扩展域并查集，把有关系的动物放到一个集合里，使每个节点与其集合的根节点产生关系，设当前节点为(x)，那么其距离(d[x] \,\, mod \,\, 3 = 0)；如果(x)可以吃根节点，那么(d[x] \,\, mod \,\, 3 = 1)；如果(x)可以被根节点吃，那么(d[x] \,\, mod \,\, 3 = 2)。那么这样每两个节点的关系都可以由它们与根节点的关系得来，如果(x，y)是同类，那说明((d[x] - d[y]) \,\, Mod \,\, 3 == 0)。

如果(x，y)是同类，那么：

1. 如果两者根节点相等但是距离不符合((d[x] - d[y]) \,\, Mod \,\, 3 ！= 0)那么说明矛盾。
2. 如果两者根节点不同那就插入到同一个集合中。
   看下图，是同类肯定满足((d[x] + d[px] - d[y]) \,\, Mod \,\, 3 == 0), 所以(d[px] = d[y] - d[x])

如果(x，y)不是同类，那么：

1. 如果两者根节点相等但是距离不符合(x)吃(y)：((d[x] - d[y] - 1) \,\, Mod \,\, 3 ！= 0)那么说明矛盾。
2. 如果两者根节点不同那就插入到同一个集合中。
   看下图，不是同类那么就得是(x)吃(y)，那么说明在(mod\,\,3)情况下，(d[x] + d[px] - d[y] = 1)，所以(d[px] = d[y] + 1 - d[x])
   

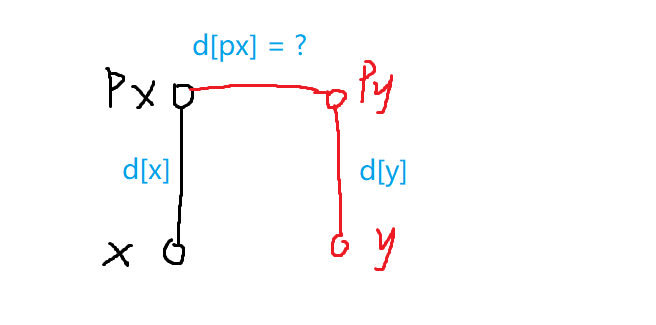
// Problem: 食物链
// Contest: AcWing
// URL: https://www.acwing.com/problem/content/description/242/
// Memory Limit: 64 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include <bits/stdc++.h>

using namespace std;

const int N = 50010;
int p[N], d[N]; 

int find(int x) {
	if (p[x] != x) {
		int t = find(p[x]);
		d[x] += d[p[x]];
		p[x] = t;
		
	}
	
	return p[x];
}

int main() {
	int n, m;
	scanf("%d%d", &n, &m);
	
	for (int i = 1; i <= n; i++) p[i] = i, d[i] = 0;
	
	int res = 0;
	while (m--) {
		int t, x, y;
		scanf("%d%d%d", &t, &x, &y);
		
		if (x > n || y > n) res++;
		else {
			int px = find(x), py = find(y);
			if (t == 1) {
				//如果是同类在一个集合中但距离不符合
				if (px == py && (d[x] - d[y]) % 3 != 0) res++; 
				else if (px != py) {
					p[px] = py;
					d[px] = d[y] - d[x];
				}
			} else {
				//如果是非同类在一个集合中判断是否满足x吃y
				if (px == py && (d[x] - d[y] - 1) % 3 != 0) res++; //非同类
				else if (px != py) {
					p[px] = py;
					d[px] = d[y] + 1 - d[x];
				}
			}
		}
	}
	
	printf("%d
", res);
	
    return 0;
}