Description
Vladik and Chloe decided to determine who of them is better at math. Vladik claimed that for any positive integer n he can represent fraction 
as a sum of three distinct positive fractions in form 
.
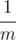Help Vladik with that, i.e for a given n find three distinct positive integers x, y and z such that 
. Because Chloe can't check Vladik's answer if the numbers are large, he asks you to print numbers not exceeding 109.
If there is no such answer, print -1.
Input
The single line contains single integer n (1 ≤ n ≤ 104).
Output
If the answer exists, print 3 distinct numbers x, y and z (1 ≤ x, y, z ≤ 109, x ≠ y, x ≠ z, y ≠ z). Otherwise print -1.
If there are multiple answers, print any of them.
Sample Input
3
7
Sample Output
2 7 42
7 8 56
思路
题意：
给出一个数 n ，问是否存在三个不同的整数 x ,y ,z 满足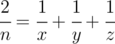
。
题解:
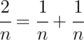，因此，我们可以让1/z = 1 / n，剩下的为 1/x + 1/y = 1/n，通过恒等变换可以知道 1/x = ny / (y - n)，可以发现，y = n + 1时候，x 必然为整数，因此x = n + n * n，y = n + 1，z = n。需要注意的是，当 n = 1时，x = 2，y = 2，不符合题意。
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n;
scanf("%d",&n);
if (n == 1) printf("-1
");
else printf("%d %d %d
",n*n + n,n + 1,n);
return 0;
}