Description:
在兰兰的模型中,神经网络就是一张有向图,图中的节点称为神经元,而且两个神经元之间至多有一条边相连,下图是一个神经元的例子:
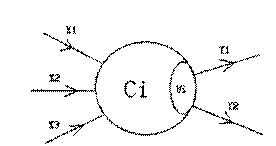
神经元〔编号为111)
图中,X1−X3X_1-X_3X1−X3是信息输入渠道,Y1−Y2Y_1-Y_2Y1−Y2是信息输出渠道,C1C_1C1表示神经元目前的状态,UiU_iUi是阈值,可视为神经元的一个内在参数。
神经元按一定的顺序排列,构成整个神经网络。在兰兰的模型之中,神经网络中的神经元分为几层;称为输入层、输出层,和若干个中间层。每层神经元只向下一层的神经元输出信息,只从上一层神经元接受信息。下图是一个简单的三层神经网络的例子。
兰兰规定,Ci服从公式:(其中n是网络中所有神经元的数目)
[C_i=∑_{j,i∈E}W_{ji}C_j−U_i
]
[公式中的W_{ji}(可能为负值)表示连接j号神经元和i号神经元的边的权值。当 C_i大于0时,该神经元处于兴奋状态,否则就处于平静状态。当神经元处于兴奋状态时,下一秒它会向其他神经元传送信号,信号的强度为C_i。
]
如此。在输入层神经元被激发之后,整个网络系统就在信息传输的推动下进行运作。现在,给定一个神经网络,及当前输入层神经元的状态(C_i),要求你的程序运算出最后网络输出层的状态。
Analysis:
显然这道题用拓扑排序,我们从入度为0的点开始遍历,一直到出度为0的点。输入层神经元被激发之后,那么u[i]为1或0都没有关系,它一定会被激活。于是我们需要预处理这种情况,并预处理出度为0的点来方便输出。
首先输入时确定是否为输入层(C[i]是否大于0),非输入层可以直接在这里减去U。根据公式,要求一个点的权值C,就要求出所有的C[j]*W[i,j],因为没有被激发的点的权值C为0,所以0乘W为0,因此不用计算。于是,所有的节点的权值是从他的上一个节点推过来的(拓扑排序),由于提前预处理了U,所以可以写成C[v] += C[u] * e[i].w,其中e[i]:u -> v。这样通过拓扑排序,C[i]的值便可以简单地累加起来了,避免了U的麻烦。
Code
#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
#define N 110
#define P 100001
using namespace std;
struct edge{
int w,to,next;
}e[P];
int head[N],U[N],C[N],in[N],out[N],num_edge,n,p;
inline void add(int u,int v,int w){
e[++num_edge].next = head[u];
e[num_edge].to = v;
e[num_edge].w = w;
head[u] = num_edge;
}
void topologicalSort(){
queue<int>Q;
for(int i = 1;i <= n;++i){
if(!in[i]){
Q.push(i);
}
}
while(!Q.empty()){
int u = Q.front();Q.pop();
for(int i = head[u];i;i = e[i].next){
int v = e[i].to;
if(!(--in[v])) Q.push(v);
if(C[u] > 0) C[v] += e[i].w*C[u];
}
}
}
void solve(){
topologicalSort();
bool tag = 1;
for(int i = 1;i <= n;++i){
// output
if(C[i] > 0 && out[i] == 0){
printf("%d %d
",i,C[i]);
tag = 0;
}
}
if(tag) printf("NULL");
}
int main(){
scanf("%d%d",&n,&p);
for(int i = 1;i <= n;++i){
scanf("%d%d",&C[i],&U[i]);
if(C[i] == 0){
C[i] -= U[i];//?
}
}
for(int i = 1;i <= p;++i){
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);
++in[v];
++out[u];
}
solve();
return 0;
}