Largest Rectangle in a Histogram-单调栈の入门典题

单调栈的好题

题目链接

题目是求最大矩形面积

---

1.BF思路

可以想到最后大矩形的上边界一定是某个小矩形的顶

那么我们就枚举每一个小矩形,

将其顶作为限制条件尽可能地向两边扩展

复杂度(O(n^2))

---

2.单调栈做法

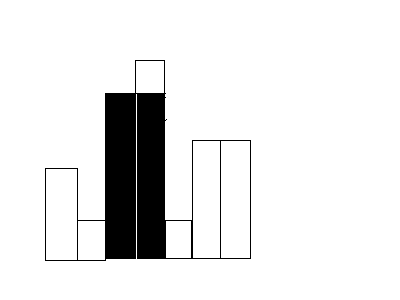
如图,黑色为最终要求的矩形

我们可以维护一个单调递增栈

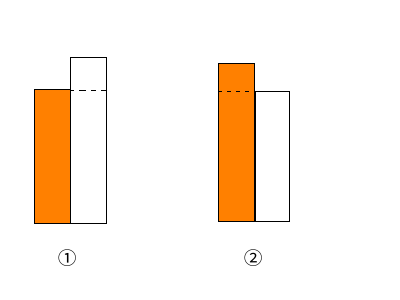
如上图:(从黄色的矩形(Y)向右扩展,假设左边所有矩形递增)

​ ①:此时右边的矩形高于左边矩形,不影响黄色矩形继续向右扩展,可以加入单调栈

​ ②:此时右边的矩形低于左边的矩形,那么以左边的矩形为最大高度的矩形不能向右扩展,于是可以向左统计答 案.又因为从左往右已经是单调递增,那么可以直接统计答案,同时将此矩形退栈.以此类推,直到栈顶元素的高度小于新加入的矩形的高度.

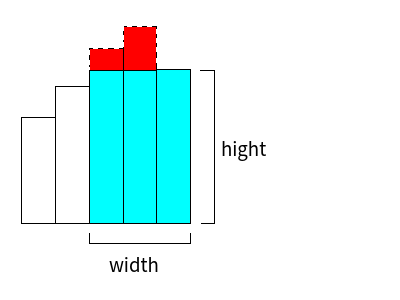
如图,最右边的矩形加入时会将左侧的两个矩形退栈,并相应地计算这两个矩形的答案.然后这两个矩形的上部(红棕色部分)可以舍弃,因为它们不会再产生任何贡献.需要注意的是,在退栈时,还要将退栈元素的宽度加起来,再赋值给新加入的矩形,那么此时最右边的矩形实际上代表图中的所有蓝色部分.当以后有更矮的矩形进栈且需要将蓝色部分退栈时,统计答案就可以直接 (hight imes width) .

这样做的正确性在于:当该矩形退栈时,其左边的第一个元素(即栈中在它以下的第一个元素)是第一个比它矮的;其右边的矩形一定比它矮(不然就不需要退栈了)

3.代码

#include<bits/stdc++.h>
#define R register int
using namespace std;
int n,h[100006],wid[100006],s[100006],top;
long long ans;//注意要开longlong
int main()
{
    while(cin>>n)
    {
        if(n==0)return 0;
        memset(s,0,sizeof(s));
        memset(h,0,sizeof(h));
        memset(wid,0,sizeof(wid));
        top=0;ans=0;//记得清零!!!
        for(R i=1;i<=n;i++)
            cin>>h[i];
        h[++n]=0;//加入一个高度为0的点,可以在最后统计答案,不会遗漏
        for(R i=1;i<=n;i++)
        {
            int width=0;
            while(top&&h[s[top]]>h[i])
            {
                width+=wid[top];
                ans=max(ans,(long long)width*h[s[top]]);
                top--;
            }
            s[++top]=i;
            wid[top]=width+1;
        }
        cout<<ans<<endl;
    }
}