一、线性表的定义
上一章我说了算法的基本概念,自我感觉还是蛮不错,接下来就是真正的数据结构的东西了,首先我们先认识线性表。那么什么是线性表呢?这个可是数据结构的基础啊(敲黑板!!!)。
线性表 (List ):零个或多个数据元素的有限序列。
这里需要强调几个关键的地方。
首先它是一个序列。 也就是说元素之间是有顺序的,若元素存在多个,则第一个元素无前驱,最后一个元素无后继,其他每个元素都有且只有一个前驱和后继。
然后,线性表强调是有限的,在计算机中处理的对象都是有限的,那种无限的数列,只存在于数学的概念中。
上面的概念不清楚,那我举个例子,银行一群排队取钱的人,那么首先是有顺序的,而且在没有新人加入的情况下,这个队伍也是有限的,同时我们要清楚,排第一个人的前面没有人(也就是无前驱),排最后的人在没有新人加入的情况下,后面是没有人的(也就是无后继),同时排中间的人前面一个人,后面一个人(一个前驱,一个后继)。
二、线性表的抽象数据类型
前面线性表的定义定下来了,那么线性表可以有什么操作呢?
以上面的列子,当这群取钱的人发现取款机没有钱了,没办法,只有换一台取款机了,那么这个队伍就为空了,这个就是线性表重置为空表的操作;然后我们看排第一个的是个男士,第二个是个女士,以此类推,这个就是根据位置查看线性表中的元素操作;然后我们数一数这个队伍有多少人,就可以发现这个队伍的长度,这个就是查看线性表长度的操作;然后忽然有人插到第一个人前面说他孩子要出生了要取钱,没办法只有让他插队,这个就是线性表的插入操作;队伍中忽然有人接到电话马上要走,没办法,只有走了,这个就是线性表的删除操作等。
所以我们根据上面的例子,线性表的抽象数据类型定义如下:
线性表的数据对象集合为 {a1,a2, …,an},每个元素的类型为 DataType。 其中除第一个元素a1外,每一个元素有且只有一个直接前驱元素,除了最后一个元素an外,每个元素有且只有一个直接后继元素。数据元素之间的关系是一对一的关系。
线性表的操作:
1、初始化操作,即建立一个新的线性表;
2、将线性表清空;
3、获取线性表的长度;
4、判断线性表是否为空;
5、插入新元素(包括在指定位置),删除元素;
6、返回线性表第n个位置的元素;
7、遍历线性表;
三、线性表的顺序存储结构
线性表一共有两种存储结构,一种是顺序存储,一种是链式存储,接下来我们就先说说顺序存储。
1、顺序存储的定义
线性表的顺序存储结构,指的是用一段地址连续的存储单元依次存储线性表的数据元素。

2、顺序存储方式
顺序存储方式其实很简单,就是在内存中找一块连续的空间,然后将相同的数据元素一次放置在这个空间中,既然线性表的每个数据元素的类型都相同,所以可以用一维数组来实现顺序存储结构, 即把第一个数据元素存到数组下标为 0 的位置中,接着把线性表相邻的元素存储在数组中相邻的位置。
3、数组长度与线性表长度区别
这里我们要明确两个概念:数组长度与线性表长度
数组的长度是存放线性表的存储空间的长度,存储分配后这个量是一般是不变的。
线性表的长度是线性表中数据元素的个数,随着线性表插入和删除操作的进行, 这个量是变化的。
在任意时刻,线性表的长度应该小于等于数组的长度。
4、数据元素与数组的对应关系
数据元素的序号和存放它的数组下标之间存在对应关系如图:
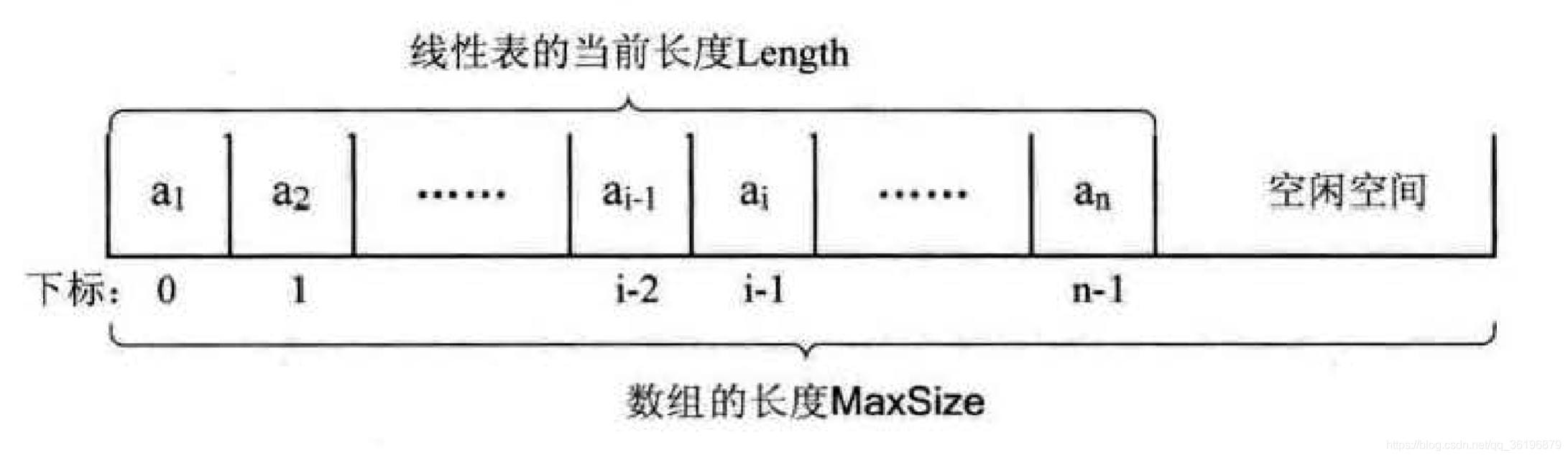
我们数组下标是从0开始计数的,但是数据元素的位置的序号是从1开始的,意思就是说数组下标为0存储的数据元素1。
用数组存储顺序表意味着要分配固定长度的数组空间,由于线位表中可以进行插入和删除操作,因此分配的数组空间要大于等于当前线性表的长度。内存中的地址,就和图书馆或电影院里的座位一样,都是有编号的,存储器中的每个存储单元都有自己的编号,这个编号称为地址,但是我们一般不关注,只需要关注数组与数据元素的对应关系就行了。
四、线性表存储结构的插入与删除
1、插入与删除
之前我们说过获取线性表的位置很简单,但是顺序表的插入和删除就比较麻烦了,就像我之前举的例子,一群银行取钱的人,忽然在中间插入一个人,后面的人肯定要后移一个位置;假如中间忽然少了一个人,后面的人就可以往前面移动一个位置,相对来说代价还是挺大的,当然在最后插入删除肯定是最简单的,接下来我们来看一段代码:
public class SeqList {
private int maxSize;// 数组的最大长度
private int size;// 数据元素的大小
private Object[] arrayList;// 对象数组,可以看作一个顺序表
public SeqList(int maxS) {// 顺序表的构造函数
maxSize = maxS;
size = 0;
arrayList = new Object[maxSize];
}
/**
* 插入方法
*
* @param index
* @param obj
* @throws Exception
*/
public void insert(int index, Object obj) throws Exception {
if (index == maxSize) {// 检测顺序表数据是否占满
throw new Exception("顺序表数据已满,无法插入数据");
}
if (index < 0 || index > size) {// 检测i插入的位置是否正确
throw new Exception("顺序表无法插入该位置");
}
if (index < size) { // 检测i插入的是否是最后一位
for (int j = size - 1; j >= index; j--) {// i位置后面的元素往后移动一位
arrayList[j + 1] = arrayList[j];
}
}
arrayList[index] = obj;
size++;
}
/**
* 删除方法
* @param index
* @return
* @throws Exception
*/
public Object delete(int index) throws Exception {
if (size == 0) {// 检测顺序表数据是否为空
throw new Exception("该线性表元素为空");
}
if (index < 0 || index > size) {// 检测删除i位置是否正确
throw new Exception("该位置无法删除元素");
}
Object obj = arrayList[index];// 保留删除的位置的元素
if (index < size) {// 检测是否是最后一位删除
for (int j = index; j <= size - 1; j++) {
arrayList[j] = arrayList[j + 1];
}
}
size--;
return obj;
}
/**
* 获取某位数据
* @param index
* @return
* @throws Exception
*/
public Object getData(int index) throws Exception {
if (index < 0 || index > size) {
throw new Exception("该位置无元素");
}
return arrayList[index];
}
/**
* 判断线性表是否为空
* @return
*/
public Object isEmpty() {// 判断该线性表是否为空
return size == 0;
}
/**
* 获取线性表长度
* @return
*/
public int getSize() {// 获取线性表元素长度
return size;
}
}
现在我们来分析一下,插入和删除的时间复杂度。
先来看最好的情况,如果元素要插入到最后一个位置, 或者删除最后一个元素, 此时时间复杂度为 O(1),因为不需要移动元素,最坏的情况呢,如果元素要插入到第一个位置或者删除第一个元素,此时时间复杂度是多少呢?那就意味着要移动所有的元素向后或者向前,所以这个时间复杂度为 O(n)。至于平均的情况,由于元素插入到第 i 个位置,或删除第 i 个元素, 需要移动 n-i 个元素。 根据概率原理, 每个位置插入或删除元素的可能性是相同的,也就说位置靠前,移动元素多,位置靠后,移动元素少。最终平均移动次数和最中间的那个元素的移动次数相等,为(n-1)/2,根据我们之前的大O记算法可知,时间复杂度为O(n)。
所以线性表的顺序存储结构,在存、读数据时,不管是哪个位置,时间复杂度都是 O(1);而插入或删除时,时间复杂度都是 O(n)。
2、线性表存储结构的优缺点
优点:
1、无须为表示表中元素之间的逻辑关系而增加额外的存储空间
2、可以快速地存取表中任一位置的元素
缺点:
1、插入和删除需要移动大量的元素
2、当线性表长度变化较大时,难以确定存储空间的容量
3、容易造成存储空间的“碎片”