转载自:https://leetcode-cn.com/problems/pascals-triangle-ii/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-by--28/
题目:
给定一个非负索引 k,其中 k ≤ 33,返回杨辉三角的第 k 行。
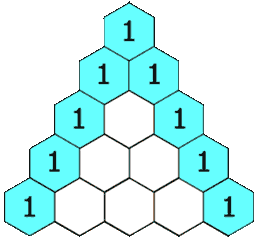
在杨辉三角中,每个数是它左上方和右上方的数的和。
示例:
输入: 3
输出: [1,3,3,1]
进阶:
你可以优化你的算法到 O(k) 空间复杂度吗?
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/pascals-triangle-ii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
和 118 题 一样,依旧是杨辉三角。区别在于之前是输出所有层的数,这道题只需要输出第 k 层的数。
解法一
和 118 题 一样,我们只需要一层一层的求。但是不需要把每一层的结果都保存起来,只需要保存上一层的结果,就可以求出当前层的结果了。
public List<Integer> getRow(int rowIndex) {
List<Integer> pre = new ArrayList<>();
List<Integer> cur = new ArrayList<>();
for (int i = 0; i <= rowIndex; i++) {
cur = new ArrayList<>();
for (int j = 0; j <= i; j++) {
if (j == 0 || j == i) {
cur.add(1);
} else {
cur.add(pre.get(j - 1) + pre.get(j));
}
}
pre = cur;
}
return cur;
}
参考 这里,其实我们可以优化一下,我们可以把 pre 的 List 省去。
这样的话,cur每次不去新建 List,而是把cur当作pre。
又因为更新当前j的时候,就把之前j的信息覆盖掉了。而更新 j + 1 的时候又需要之前j的信息,所以在更新前,我们需要一个变量把之前j的信息保存起来。
public List<Integer> getRow(int rowIndex) {
int pre = 1;
List<Integer> cur = new ArrayList<>();
cur.add(1);
for (int i = 1; i <= rowIndex; i++) {
for (int j = 1; j < i; j++) {
int temp = cur.get(j);
cur.set(j, pre + cur.get(j));
pre = temp;
}
cur.add(1);
}
return cur;
}
区别在于我们用了 set 函数来修改值,由于当前层比上一层多一个元素,所以对于最后一层的元素如果用 set 方法的话会造成越界。此外,每层的第一个元素始终为1。基于这两点,我们把之前j == 0 || j == i的情况移到了for循环外进行处理。
除了上边优化的思路,还有一种想法,那就是倒着进行,这样就不会存在覆盖的情况了。
因为更新完j的信息后,虽然把j之前的信息覆盖掉了。但是下一次我们更新的是j - 1,需要的是j - 1和j - 2 的信息,j信息覆盖就不会造成影响了。
public List<Integer> getRow(int rowIndex) {
int pre = 1;
List<Integer> cur = new ArrayList<>();
cur.add(1);
for (int i = 1; i <= rowIndex; i++) {
for (int j = i - 1; j > 0; j--) {
cur.set(j, cur.get(j - 1) + cur.get(j));
}
cur.add(1);//补上每层的最后一个 1
}
return cur;
}
解法二 公式法
如果熟悉杨辉三角,应该记得杨辉三角其实可以看做由组合数构成。
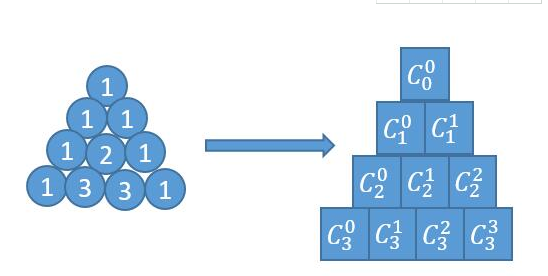
根据组合数的公式,将(n-k)!约掉,化简就是下边的结果。
C^k_n = n!/(k!(n-k)!) = (n*(n-1)*(n-2)*...(n-k+1))/k!
C
n
k
=n!/(k!(n−k)!)=(n∗(n−1)∗(n−2)∗...(n−k+1))/k!
然后我们就可以利用组合数解决这道题。
public List<Integer> getRow(int rowIndex) {
List<Integer> ans = new ArrayList<>();
int N = rowIndex;
for (int k = 0; k <= N; k++) {
ans.add(Combination(N, k));
}
return ans;
}
private int Combination(int N, int k) {
long res = 1;
for (int i = 1; i <= k; i++)
res = res * (N - k + i) / i;
return (int) res;
}
参考 这里,我们可以优化一下。
上边的算法对于每个组合数我们都重新求了一遍,但事实上前后的组合数其实是有联系的。
C_n^k=C_n^{k-1} imes(n-k+1)/k
C
n
k
=C
n
k−1
×(n−k+1)/k
代码的话,我们只需要用pre变量保存上一次的组合数结果。计算过程中,可能越界,所以用到了long。
public List<Integer> getRow(int rowIndex) {
List<Integer> ans = new ArrayList<>();
int N = rowIndex;
long pre = 1;
ans.add(1);
for (int k = 1; k <= N; k++) {
long cur = pre * (N - k + 1) / k;
ans.add((int) cur);
pre = cur;
}
return ans;
}
总
这道题其实还是比较简单的,只是优化的两种方法是比较常用的,一种就是用pre变量将要被覆盖的变量存起来,另一种就是倒着进行。另外求组合数的时候,要防止int的溢出。
之前自己在博客总结的,更多题解可以在原地址 https://leetcode.wang。
作者:windliang
链接:https://leetcode-cn.com/problems/pascals-triangle-ii/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-by--28/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。