Description
gty又虐了一场比赛,被虐的蒟蒻们决定吊打gty。
gty见大势不好机智的分出了n个分身,但还是被人多势众的蒟蒻抓住了。
蒟蒻们将n个gty吊在n根绳子上,每根绳子穿过天台的一个洞。
这n根绳子有一个公共的绳结x。
吊好gty后蒟蒻们发现由于每个gty重力不同,绳结x在移动。
蒟蒻wangxz脑洞大开的决定计算出x最后停留处的坐标,由于他太弱了决定向你求助。
不计摩擦,不计能量损失,由于gty足够矮所以不会掉到地上。
Input
输入第一行为一个正整数n(1<=n<=10000),表示gty的数目。
接下来n行,每行三个整数xi,yi,wi,表示第i个gty的横坐标,纵坐标和重力。
对于20%的数据,gty排列成一条直线。
对于50%的数据,1<=n<=1000。
对于100%的数据,1<=n<=10000,-100000<=xi,yi<=100000
Output
输出1行两个浮点数(保留到小数点后3位),表示最终x的横、纵坐标。
Sample Input
3
0 0 1
0 2 1
1 1 1
0 0 1
0 2 1
1 1 1
Sample Output
0.577 1.000
题解Here!
一看,这道题好像无从下手。。。
根据物理学知识,当系统处于平衡状态时,系统的总能量最小。
这里只有重力势能 Ep 。
并且 Ep=mgh 。
所以,只要使得 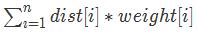 也就是总的重力势能最小,就可以使系统平衡。
也就是总的重力势能最小,就可以使系统平衡。
于是,模拟退火横空出世!
模拟退火最主要的参数有几个:
T0, 初始温度.
t, 每一次下降的温度.
ans, 目前为止最优的答案.
now, 新的状态.
delta, 当前答案与最优答案的差值.
但是,还有一点,模拟退火得到答案后,还要在附近的点中再取1000~2000个点,更新答案。
附代码:
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cmath>
#define MAXN 10010
using namespace std;
int n;
double minn=(1LL<<62);
struct node{
double x,y,weight;
}ans,a[MAXN];
inline int read(){
int date=0,w=1;char c=0;
while(c<'0'||c>'9'){if(c=='-')w=-1;c=getchar();}
while(c>='0'&&c<='9'){date=date*10+c-'0';c=getchar();}
return date*w;
}
inline double get_random(){return rand()%10000/10000.0;}
inline double Ep(node now){
double sum=0;
for(int i=1;i<=n;i++)sum+=sqrt((now.x-a[i].x)*(now.x-a[i].x)+(now.y-a[i].y)*(now.y-a[i].y))*a[i].weight;
if(sum<minn){ans=now;minn=sum;}
return sum;
}
void SA(){
double T=100000.0;
node t=ans;
while(T>0.001){
node now;
now.x=t.x+(get_random()*2-1.0)*T;
now.y=t.y+(get_random()*2-1.0)*T;
double delta=Ep(t)-Ep(now);
if(delta>0||exp(delta/T)>get_random())t=now;
T*=0.991;
}
for(int i=1;i<=1000;i++){
node now;
now.x=ans.x+(get_random()*2-1.0)*T;
now.y=ans.y+(get_random()*2-1.0)*T;
Ep(now);
}
}
int main(){
srand(2002);
n=read();
for(int i=1;i<=n;i++){
a[i].x=read();a[i].y=read();a[i].weight=read();
ans.x+=a[i].x;ans.y+=a[i].y;
}
ans.x/=(double)n;ans.y/=(double)n;
SA();
printf("%.3lf %.3lf
",ans.x,ans.y);
return 0;
}