看代码:
1 int cal(int n) { 2 int sum = 0; 3 int i = 1; 4 for (; i <= n; ++i) { 5 sum = sum + i; 6 } 7 return sum; 8 }
从cpu角度来看,这段代码每一行都执行类似操作 读数据-运算-写数据 ,
现在假设每行代码执行时间都为unit_time。在这个假设的基础上,我们看看上面这个代码块的用时

经过分析得出用时为(1+1+n+n)*unit_time,也就是(2+2n)*unit_time,可以看出 n越大,时间花费越多,并且成正比
再看这段代码
1 int cal(int n) { 2 int sum = 0; 3 int i = 1; 4 int j = 1; 5 for (; i <= n; ++i) { 6 j = 1; 7 for (; j <= n; ++j) { 8 sum = sum + i * j; 9 } 10 } 11 }
分析一下花费时间

花费时间为(1+1+1+n+n+n^2+n^2)*unit_time 也就是(3+2n+2n^2)*unit_time
以上的分析可以总结为一个公式:T(n)=O(f(n)) f(n)表示每行代码执行的次数总和,n表示数据规模大小
现在假设这种情况,n为1000万,那n^2 就是100亿。1000万在100亿面前不值一提,直接可以无视,而常数1,2,3,10000这些小打小闹的数在1000万面前不值一提,更别说在100亿面前。
所以上面的第一个时间复杂度O(2+2n)中,我们可以将常数直接忽略掉。即为O(n)
第二个时间复杂度O(3+2n+2n^2),在n^2面前,前两个不足为提,直接忽略掉,即为O(n^2)
时间复杂度分析:
1)只关注循环执行次数最多的一段代码

2)加法法则:总复杂度等于量级最大的那段代码的复杂度

3)3. 乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

接下来我们看第三个代码片段:
1 i=1; 2 while (i <= n) { 3 i = i * 2; 4 }
第三行代码是循环执行次数最多的。所以,我们只要能计算出这行代码被执行了多少次,就能知道整段代码的时间复杂度。
从代码中可以看出,变量 i 的值从 1 开始取,每循环一次就乘以 2。当大于 n 时,循环结束。还记得我们高中学过的等比数列吗?实际上,变量 i 的取值就是一个等比数列。如果我把它一个一个列出来,就应该是这个样子的:
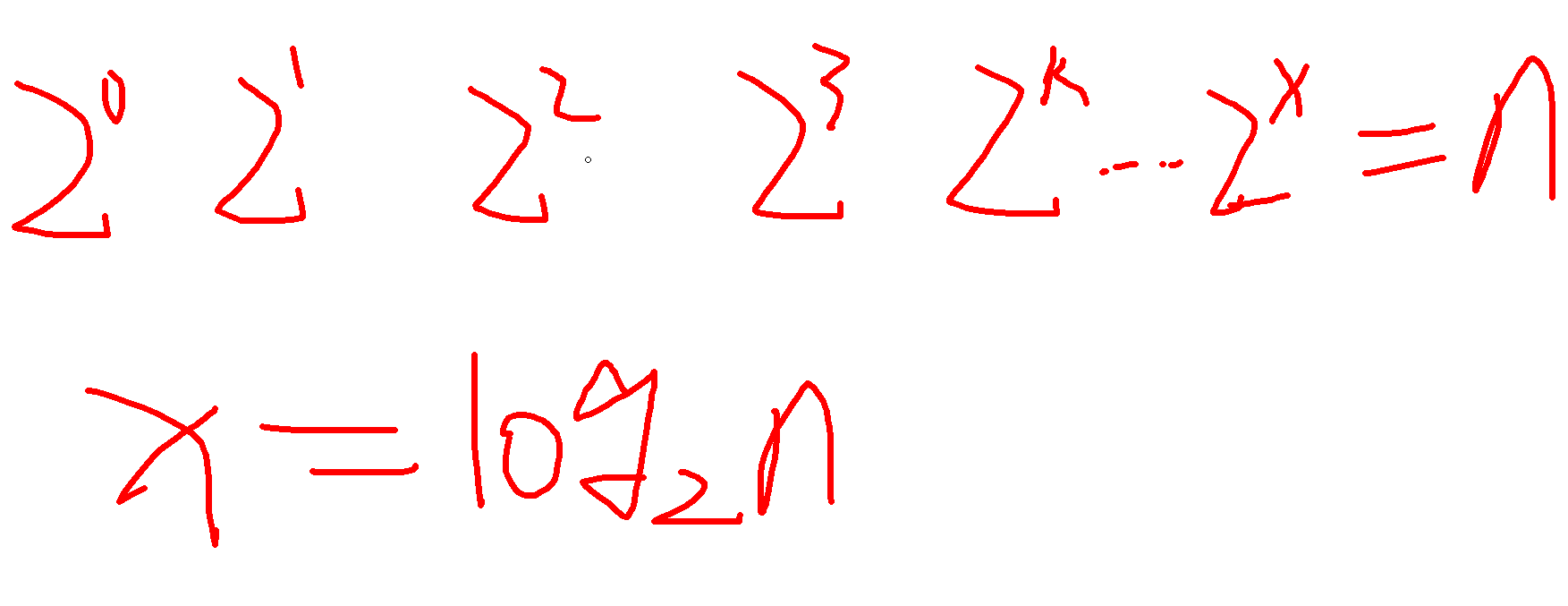
所以时间复杂度为![]() 。
。
再看下面代码:
1 i=1; 2 while (i <= n) { 3 i = i * 3; 4 }
用上面的分析,分析出时间复杂度应该为![]()
我们知道,对数之间是可以互相转换的,log3n 就等于 log32 * log2n,所以 O(log3n) = O(C * log2n),其中 C=log32 是一个常量。基于我们前面的一个理论:在采用大 O 标记复杂度的时候,可以忽略系数,即 O(Cf(n)) = O(f(n))。所以,O(log2n) 就等于 O(log3n)。因此,在对数阶时间复杂度的表示方法里,我们忽略对数的“底”,统一表示为 O(logn)。
空间复杂度分析相对就简单了,占多少内存就是多少
1 void print(int n) { 2 int i = 0; 3 int[] a = new int[n]; 4 for (i; i <n; ++i) { 5 a[i] = i * i; 6 } 7 8 for (i = n-1; i >= 0; --i) { 9 print out a[i] 10 } 11 }
第 2 行代码中,我们申请了一个空间存储变量 i,但是它是常量阶的,跟数据规模 n 没有关系,所以我们可以忽略。第 3 行申请了一个大小为 n 的 int 类型数组,除此之外,剩下的代码都没有占用更多的空间,所以整段代码的空间复杂度就是 O(n)。
常见的空间复杂度就是 O(1)、O(n)、O(n2 ),像 O(logn)、O(nlogn) 这样的对数阶复杂度平时都用不到