[Poi2010] Antisymmetry

2084: [Poi2010]Antisymmetry

Time Limit: 10 Sec  Memory Limit: 259 MB
Submit: 1205  Solved: 756
[Submit][Status][Discuss]

Description

对于一个01字符串，如果将这个字符串0和1取反后，再将整个串反过来和原串一样，就称作“反对称”字符串。比如00001111和010101就是反对称的，1001就不是。
现在给出一个长度为N的01字符串，求它有多少个子串是反对称的。

Input

第一行一个正整数N (N <= 500,000)。第二行一个长度为N的01字符串。

Output

一个正整数，表示反对称子串的个数。

Sample Input

8
11001011

Sample Output

7

hint
7个反对称子串分别是：01(出现两次), 10(出现两次), 0101, 1100和001011

HINT

 

Source

鸣谢 JZP

题意：

求一个01串中“反回文”子串的个数。“反回文”的定义为$str(i)=!str(N-i+1)$。

题解：

这道题枚举回文子串中间位置+二分答案即可AC，但实际上存在一种名为$Manacher$的线性算法。

我记得我个人解决回文子串问题的复杂度从$O(N^3)$到$O(N^2)$再到$O(NlogN)$不断进步，这次终于达到理论上的下限了……

（以下图片全部转自CSDN某dalao，侵删）

一般的回文串算法都是枚举回文串的中心位置然后分奇偶讨论。但$Manacher$算法提供了一种巧妙的方法使得可以将奇偶回文串在一起处理。

具体方法是在原串每两个字符间插入一个分隔符，再在头尾分别插入一个分隔符，分隔符要求不在原串中出现。如下：

然后我们考虑设$len(i)$表示在新串中以$i$为中心的回文串向右延伸的长度。如下：

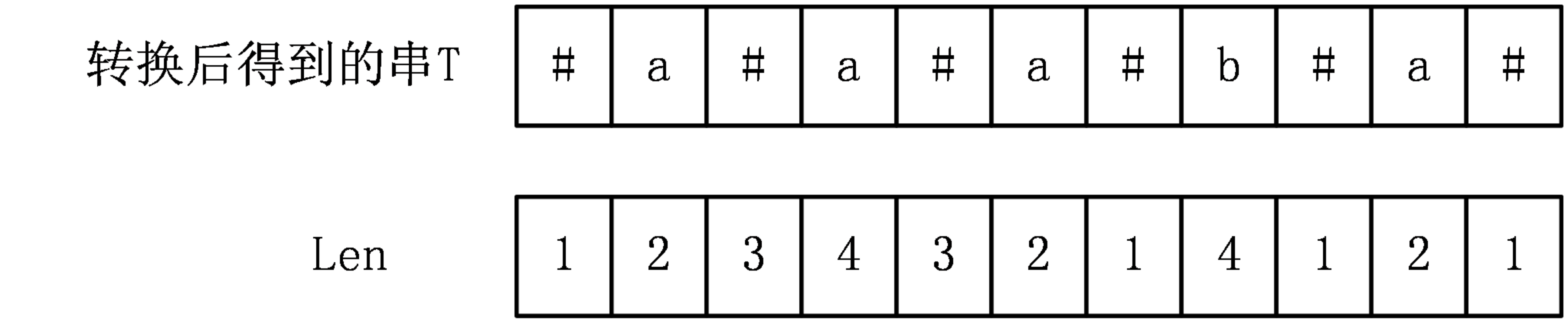
接着归纳求解，假设我们已经求出了$len(1)—len(i-1)$的值，现在要求$len(i)$，记其中向右延伸到的位置最远的$len(Po)$为$P$（与扩展kmp神似），有如下几种情况：

若$i<=P$，那么找到$i$相对于$po$的对称位置$j$，如果$len[j]<=P-i$，如图：

此时由对称性可得$len[i]=len[j]$。

如果$len[j]>P-i$，如图：

此时$len[i]$至少为$P-$i，由于$i$右边的字符没有被匹配过，我们需要依次匹配并更新$Po$与$P$。

若$i>P$，如图：

此时之前处理的信息对$i$没有什么用，我们仍然需要依次匹配并更新。

$Manacher$算法每次新匹配$k$个位置，匹配完即退出。每个位置会被计算且仅被计算一次，所以该算法的复杂度是线性的。

这道题即是$Manacher$算法的模板，只需要把匹配运算修改一下即可。

代码：

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>

using namespace std;
#define MAXN 500005
#define MAXM 500005
#define INF 0x7fffffff
#define ll long long

char tp[MAXN],str[MAXN<<1|1];
ll len[MAXN<<1|1];
inline ll read(){
    ll x=0,f=1;
    char c=getchar();
    for(;!isdigit(c);c=getchar())
        if(c=='-')
            f=-1;
    for(;isdigit(c);c=getchar())
        x=x*10+c-'0';
    return x*f;
}

inline void solve(ll N){
    for(ll i=1;i<=N;i++)
        str[(i<<1)-1]='#',str[i<<1]=tp[i];
    str[N<<1|1]='#';str[0]='!';str[(N<<1|1)+1]='?';
    return;
}
inline bool check(char x,char y){return (x=='#'&&y=='#')||(((x-'0')^(y-'0'))==1);}
inline ll Manacher(ll N){
    ll pos=0,lag=0,ans=0;
    for(ll i=1;i<=N;i++){
        len[i]=(i<lag)?min(lag-i+1,len[(pos<<1)-i]):0;
        while(check(str[i+len[i]],str[i-len[i]])) len[i]++;
        if(i+len[i]-1>lag) lag=i+len[i]-1,pos=i;
        ans+=len[i]>>1;//cout<<len[i]<<endl;
    }return ans;
}

int main(){
    ll N=read();cin>>tp+1;solve(N);
    printf("%lld
",Manacher(N<<1|1));
    return 0;
}