差分约束问题:
给定$n$个变量${x_0,x_1,x_2,ldots,x_{n-1}}$和m个形如$x_i-x_jleq a_i(x_i-x_jgeq a_i)$的不等式,求$x_{n-1}-x_0$的最大(小)值。
例如$n=4,m=5$,不等式如图,求$x_3-x_0$的最大值。
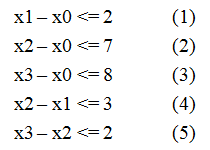
考虑初中数学方法,我们可以通过不等式相加得到一些形如$x_3-x_0leq b_i$的不等式,易得$min{b_i}$即为所求最大值。
于是暴力手算得到以下三个不等式:
1.由$(5)+(4)+(1)$得到$x_3-x_0leq7$。
2.由$(5)+(2)$得到$x_3-x_0leq9$。
3.由$(3)$得到$x_3-x_0leq8$。
联立解得$x_3-x_0leq7$,最大值为$7$。
我不知道是否有人认为手算十分简便,不过我现在写起来感觉十分恶心。
那么如何系统解决这类问题呢?
考虑另一个问题,给定一张有四个点,五条边的有向图,如图所示:
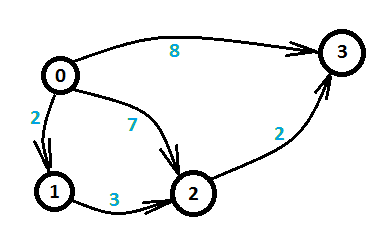
(图源网络,侵删)
求第$0$个点到第$3$个点的最短路。
显然答案是$7$,根本不用进行什么演算。
那么这两个问题间有什么关联呢?
考虑我们将第一个问题中一些不等式的和转化为$x_{n-1}-x_0leq b_i$的过程。
若只转换成一个不等式,即由$x_{n-1}-x_ileq a_i,x_i-x_jleq a_j,ldots,x_k-x_0leq a_0$求和可得$x_{n-1}-x_0leq sum a_i$。
那么这样的一个过程是否等价于,在图上沿$x_0 ightarrow x_k,ldots,x_j ightarrow x_i,x_i ightarrow x_{n-1}$这些边走出的一条$x_0$到$x_{n-1}$,花费$sum a_i$的路径?
显然的,转换不等式的过程中等式右边的值每次增加$a_i$,最终为$x_{n-1}-x_0leq sum a_i$,所求的是最大值所以等号取等,两者便等价了。
那么我们推广成$K$个不等式的情况,即将$x_{n-1}-x_0leq b_0,x_{n-1}-x_0leq b_1,ldots,x_{n-1}-x_0leq b_K$这些不等式转化成图上$x_0 ightarrow x_{n-1}$长度为$b_0,b_1,ldots,b_K$的路径。
此时可以发现$max{x_{n-1}-x_0}=min{b_i}$,即图上从$x_0$到$x_{n-1}$的最短路径的长度。
问题转化成功。现在我们只需要打一个最短路板子就可以解决这个手算量$MAX$的差分约束问题了。
一般地,差分约束问题总可以转化为最短(长)路问题求解。(求最大值跑最短路,求最小值跑最长路)
将每个形如$x_i-x_jleq a_i(x_i-x_jgeq a_i)$的不等式转化成图上$j ightarrow i$,权值为$a_i$的边,以$0$为起点进行单原最短(长)路算法求解即可,答案为$dis_{n-1}$。
(以最短路为例)最终图中必定满足对于任意$i,j$,如果有$j ightarrow i$,权值$a_i$的边存在,则$dis_ileq dis_j+a_i$,严格满足差分约束。
反之,如果$0 ightarrow n-1$的路径中存在负环(存在形如$x_i-x_jgeq a$与$x_i-x_j<a$的一组等式)或者$0$和$n-1$不连通($x_{n-1}$不受$x_0$的约束条件影响),则原问题无解。
在算法竞赛中,差分约束系统的不等式约束关系一般是不明显的,需要我们自己抽象出模型进行解答。
模板题目:poj1201
题意:从 $0sim 5 imes 10^4$ 中选出尽量少的整数,使每个区间 $[a_i,b_i]$ 内都有至少 $c_i$ 个数被选出。
题解:设 $s_i$ 表示 $0sim i$ 中选了多少整数,然后转化成三角形不等式即可。
代码:
#include<algorithm> #include<iostream> #include<cstring> #include<cstdio> #include<queue> using namespace std; #define MAXN 1000005 #define MAXM 50000 #define INF 0x7fffffff #define ll long long int hd[MAXN],to[MAXN<<1],cnt; int cst[MAXN<<1],nxt[MAXN<<1]; int dis[MAXN];bool inq[MAXN]; inline int read(){ int x=0,f=1; char c=getchar(); for(;!isdigit(c);c=getchar()) if(c=='-') f=-1; for(;isdigit(c);c=getchar()) x=x*10+c-'0'; return x*f; } inline void addedge(int u,int v,int w){ to[++cnt]=v,cst[cnt]=w; nxt[cnt]=hd[u],hd[u]=cnt; return; } inline void SPFA(int s){ memset(dis,-63,sizeof(dis)); queue<int> q;q.push(s); dis[s]=0,inq[s]=1; while(!q.empty()){ int u=q.front(); q.pop();inq[u]=0; for(int i=hd[u];i;i=nxt[i]) if(dis[to[i]]<dis[u]+cst[i]){ dis[to[i]]=dis[u]+cst[i]; if(!inq[to[i]]) inq[to[i]]=1,q.push(to[i]); } } return; } int main(){ int N=read(); for(int i=1;i<=N;i++){ int u=read(),v=read(),w=read(); addedge(u-1,v,w); } for(int u=0;u<=MAXM;u++) addedge(u,u+1,0),addedge(u+1,u,-1); SPFA(0); printf("%d ",dis[MAXM]); return 0; }