题目描述
现在小朋友们最喜欢的"喜羊羊与灰太狼",话说灰太狼抓羊不到,但抓兔子还是比较在行的,而且现在的兔子还比较笨,它们只有两个窝,现在你做为狼王,面对下面这样一个网格的地形:
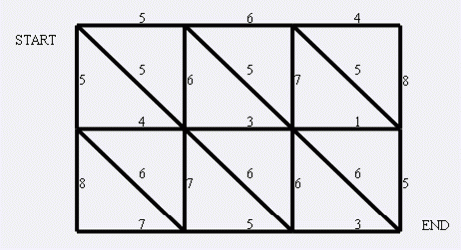
左上角点为(1,1),右下角点为(N,M)(上图中N=3,M=4).有以下三种类型的道路
1:(x,y)<==>(x+1,y)
2:(x,y)<==>(x,y+1)
3:(x,y)<==>(x+1,y+1)
道路上的权值表示这条路上最多能够通过的兔子数,道路是无向的. 左上角和右下角为兔子的两个窝,开始时所有的兔子都聚集在左上角(1,1)的窝里,现在它们要跑到右下角(N,M)的窝中去,狼王开始伏击这些兔子.当然为了保险起见,如果一条道路上最多通过的兔子数为K,狼王需要安排同样数量的K只狼,才能完全封锁这条道路,你需要帮助狼王安排一个伏击方案,使得在将兔子一网打尽的前提下,参与的狼的数量要最小。因为狼还要去找喜羊羊麻烦。
输入输出格式
输入格式:第一行为N,M.表示网格的大小,N,M均小于等于1000.
接下来分三部分
第一部分共N行,每行M-1个数,表示横向道路的权值.
第二部分共N-1行,每行M个数,表示纵向道路的权值.
第三部分共N-1行,每行M-1个数,表示斜向道路的权值.
输出格式:输出一个整数,表示参与伏击的狼的最小数量.
输入输出样例
输入样例#1:
复制
3 4 5 6 4 4 3 1 7 5 3 5 6 7 8 8 7 6 5 5 5 5 6 6 6
输出样例#1: 复制
14
把网格平面图转为对偶图
求最小割就转化为最短路
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #include<algorithm> 6 #include<queue> 7 using namespace std; 8 typedef long long lol; 9 struct Node 10 { 11 int next,to; 12 lol dis; 13 }edge[6000001]; 14 int head[2000001],num; 15 lol dist[2000001],ans; 16 int S,T,n,m,up[1001][1001],down[1001][1001],cnt; 17 bool vis[2000001]; 18 queue<int>Q; 19 lol gi() 20 { 21 char ch=getchar(); 22 lol x=0; 23 while (ch<'0'||ch>'9') ch=getchar(); 24 while (ch>='0'&&ch<='9') 25 { 26 x=x*10+ch-'0'; 27 ch=getchar(); 28 } 29 return x; 30 } 31 void add(int u,int v,lol dis) 32 { 33 num++; 34 edge[num].next=head[u]; 35 head[u]=num; 36 edge[num].to=v; 37 edge[num].dis=dis; 38 num++; 39 edge[num].next=head[v]; 40 head[v]=num; 41 edge[num].to=u; 42 edge[num].dis=dis; 43 } 44 void SPFA() 45 {int i; 46 memset(dist,127/2,sizeof(dist)); 47 Q.push(S); 48 dist[S]=0; 49 while (Q.empty()==0) 50 { 51 int u=Q.front(); 52 Q.pop(); 53 vis[u]=0; 54 for (i=head[u];i;i=edge[i].next) 55 { 56 int v=edge[i].to; 57 if (dist[v]>dist[u]+edge[i].dis) 58 { 59 dist[v]=dist[u]+edge[i].dis; 60 if (vis[v]==0) 61 { 62 vis[v]=1; 63 Q.push(v); 64 } 65 } 66 } 67 } 68 } 69 int main() 70 {int i,j,x; 71 cin>>n>>m; 72 if (n==1&&m==1) 73 { 74 cout<<0; 75 return 0; 76 } 77 if (n==1||m==1) 78 { 79 if (m==1) swap(n,m); 80 ans=2e9; 81 for (i=1;i<m;i++) 82 { 83 x=gi(); 84 if (ans>x) ans=x; 85 } 86 cout<<ans; 87 return 0; 88 } 89 S=0; 90 for (i=1;i<n;i++) 91 { 92 for (j=1;j<m;j++) 93 { 94 up[i][j]=++cnt; 95 down[i][j]=++cnt; 96 } 97 } 98 T=++cnt; 99 for (i=1;i<=n;i++) 100 { 101 for (j=1;j<m;j++) 102 { 103 x=gi(); 104 if (i==1) add(S,up[1][j],x); 105 if (i==n) add(down[n-1][j],T,x); 106 if (i!=1&&i!=n) 107 add(down[i-1][j],up[i][j],x); 108 } 109 } 110 for (i=1;i<n;i++) 111 { 112 for (j=1;j<=m;j++) 113 { 114 x=gi(); 115 if (j==1) add(down[i][1],T,x); 116 if (j==m) add(S,up[i][m-1],x); 117 if (j!=1&&j!=m) 118 add(down[i][j],up[i][j-1],x); 119 } 120 } 121 for (i=1;i<n;i++) 122 { 123 for (j=1;j<m;j++) 124 { 125 x=gi(); 126 add(up[i][j],down[i][j],x); 127 } 128 } 129 SPFA(); 130 printf("%lld",dist[T]); 131 }