题目描述
栋栋有一块长方形的地,他在地上种了一种能量植物,这种植物可以采集太阳光的能量。在这些植物采集能量后,栋栋再使用一个能量汇集机器把这些植物采集到的能量汇集到一起。
栋栋的植物种得非常整齐,一共有n列,每列有m棵,植物的横竖间距都一样,因此对于每一棵植物,栋栋可以用一个坐标(x, y)来表示,其中x的范围是1至n,表示是在第x列,y的范围是1至m,表示是在第x列的第y棵。
由于能量汇集机器较大,不便移动,栋栋将它放在了一个角上,坐标正好是(0, 0)。
能量汇集机器在汇集的过程中有一定的能量损失。如果一棵植物与能量汇集机器连接而成的线段上有k棵植物,则能 量的损失为2k + 1。例如,当能量汇集机器收集坐标为(2, 4)的植物时,由于连接线段上存在一棵植物(1, 2),会产生3的能量损失。注意,如果一棵植物与能量汇集机器连接的线段上没有植物,则能量损失为1。现在要计算总的能量损失。
下面给出了一个能量采集的例子,其中n = 5,m = 4,一共有20棵植物,在每棵植物上标明了能量汇集机器收集它的能量时产生的能量损失。
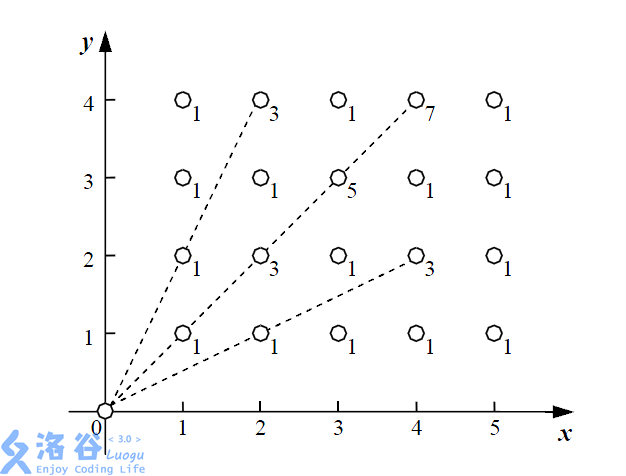
在这个例子中,总共产生了36的能量损失。
输入输出格式
输入格式:仅包含一行,为两个整数n和m。
输出格式:仅包含一个整数,表示总共产生的能量损失。
输入输出样例
【样例输入1】 5 4 【样例输入2】 3 4
【样例输出1】 36 【样例输出2】 20
说明
对于10%的数据:1 ≤ n, m ≤ 10;
对于50%的数据:1 ≤ n, m ≤ 100;
对于80%的数据:1 ≤ n, m ≤ 1000;
对于90%的数据:1 ≤ n, m ≤ 10,000;
对于100%的数据:1 ≤ n, m ≤ 100,000。
如果gcd(x,y)=d,那么(x,y)到(0,0)显然经过了这些点
gcd(x,y)=1,gcd(x,y)=2....gcd(x,y)=d-1
所以列出
$2 imessum_{i=1}^nsum_{j=1}^mgcd(i,j)-n*m$
反演分块,这道题甚至不需要考虑复杂度,因为n<=100000
O(√n*√n)数论分块套一个数论分块直接就行了
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cmath> 6 using namespace std; 7 typedef long long lol; 8 lol mu[100001],prime[100001],n,m,tot,N,M,as,ans; 9 bool vis[100001]; 10 void pre() 11 {lol i,j; 12 mu[1]=1; 13 for (i=2;i<=n;i++) 14 { 15 if (vis[i]==0) 16 { 17 prime[++tot]=i; 18 mu[i]=-1; 19 } 20 for (j=1;j<=tot;j++) 21 { 22 if (i*prime[j]>n) break; 23 vis[i*prime[j]]=1; 24 if (i%prime[j]==0) 25 { 26 mu[i*prime[j]]=0; 27 break; 28 } 29 else mu[i*prime[j]]=-mu[i]; 30 } 31 } 32 for (i=1;i<=n;i++) 33 mu[i]+=mu[i-1]; 34 } 35 lol query(int d) 36 {lol i,pos; 37 N=n/d;M=m/d; 38 as=0; 39 for (i=1;i<=N;i=pos+1) 40 { 41 pos=min(N/(N/i),M/(M/i)); 42 as+=(mu[pos]-mu[i-1])*(N/i)*(M/i); 43 } 44 return as; 45 } 46 int main() 47 {lol i,pos; 48 cin>>n>>m; 49 if (n>m) swap(n,m); 50 pre(); 51 for (i=1;i<=n;i=pos+1) 52 { 53 pos=min(n/(n/i),m/(m/i)); 54 ans+=((pos+i)*(pos-i+1)/2)*query(i); 55 } 56 ans=ans*2-n*m; 57 cout<<ans; 58 }