[AHOI2012]树屋阶梯

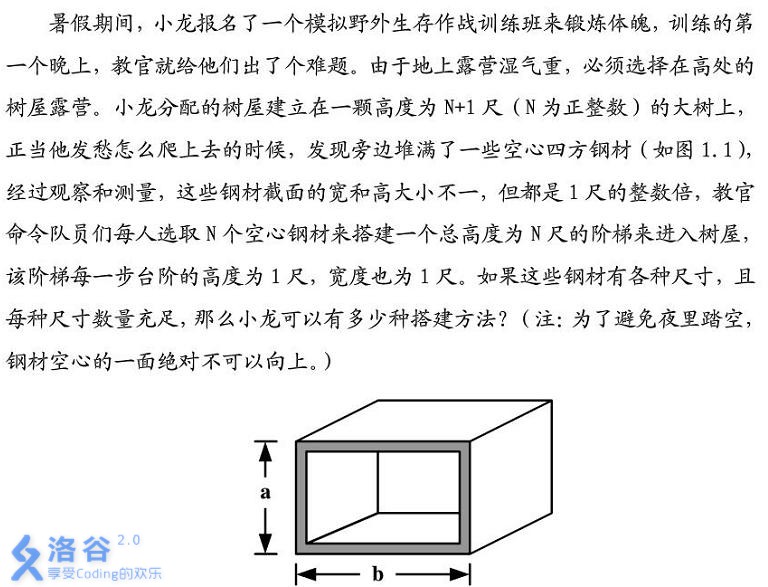
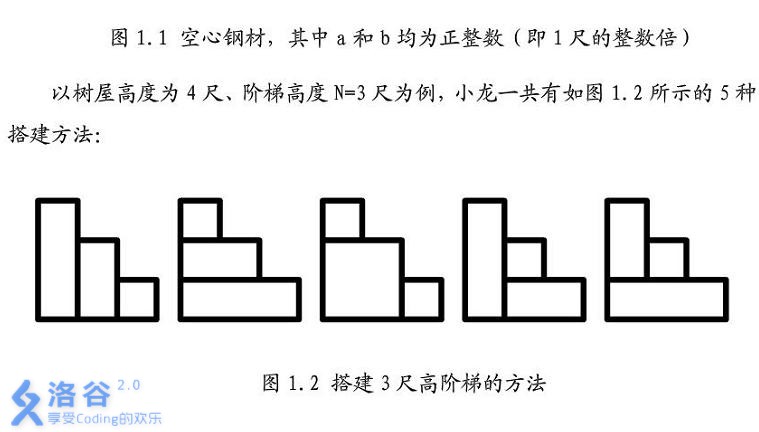
题目描述

输入输出格式

输入格式：

一个正整数N（1<=N<=500），表示阶梯的高度。

输出格式：

一个正整数，表示搭建方法的个数。（注：搭建方法的个数可能很大）

输入输出样例

输入样例#1： 复制

3

输出样例#1： 复制

5

说明

40%的数据：1<=N<=20

80%的数据：1<=N<=300

100%的数据：1<=N<=500

转载自Navi_Gayson:http://www.cnblogs.com/NaVi-Awson/p/7748308.html

我们令$C_n$表示用$n$个长方形拼成$size$为$n$的三角梯形的方案数。

如题中的图，我们枚举最左下角的点属于哪个长方形。显然有$n$种可能，每种方法又把剩下的部分分成两个三角梯形（$size$可能为$0$）。

显然我们得到

$$Catalan_n = sum _{i = 0} ^{n-1} Catalan_i * Catalan_{n-1-i}$$

其实就是$Catalan$的递推式，我们用通项公式求$Catalan_n$即可。

Catalan_n=C(n,2n)/(n+1)

学习一下Catalan，顺便复习一下重载运算符

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
int n;
struct Big_num
{
  int a[10005],len;
  Big_num(){}
  Big_num &operator *= (const int &b)
  {int i;
    for (i=1;i<=len;i++)
      a[i]*=b;
    for (i=1;i<=len;i++)
      a[i+1]+=a[i]/10,a[i]%=10;
    while (a[len+1]) 
      {
    len++;
    a[len+1]+=a[len]/10;
    a[len]%=10;
      }
  }
  Big_num &operator /=(const int b)
  {
    int now=0,i;
    Big_num ans;
    for (i=len;i>=1;i--)
    {
      now=now*10+a[i];
      if (now>=b) ans.a[i]=now/b,now%=b;
      else ans.a[i]=0;
    }
    while (ans.a[len]==0)
    len--;
    for (i=1;i<=len;i++) a[i]=ans.a[i];
   }
  void print()
  {int i;
    for (i=len;i>=1;i--)
      printf("%d",a[i]);
    cout<<endl;
  }
}Ans;
int main()
{int i;
  cin>>n;
  Ans.len=Ans.a[1]=1;
  for (i=n+2;i<=2*n;i++) Ans*=i;
  for (i=2;i<=n;i++)
    Ans/=i;
  Ans.print();
}