Description

Input

Output

Sample Input
3
1 3 2
Sample Output
1
HINT
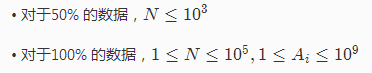
这里要用到一种技巧:
我们认为改出来的数要是整数情况下:
a[i]>a[i-1]等价于a[i]-i>=a[i-1]-i+1
这样求最长不下降子序列就行了
因为当j<i a[j]-j==a[i]-i时,说明他们中间可以填的数有i-j+1个,需要的正好也是i-j+1
所以这样是肯定可以的
如果不处理就求最长上升子序列,可能会出现中间部分无数可以填入(所以只适用于填实数)
nlogn求最长不下降有很多方法,这里用的是离散+线段树
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 int c[400001],sz; 7 int a[100001],b[100001],n,ans,f[100001]; 8 void pushup(int rt) 9 { 10 c[rt]=max(c[rt*2],c[rt*2+1]); 11 } 12 void update(int rt,int l,int r,int x,int d) 13 { 14 if (l==r) 15 { 16 c[rt]=d; 17 return; 18 } 19 int mid=(l+r)/2; 20 if (x<=mid) update(rt*2,l,mid,x,d); 21 else update(rt*2+1,mid+1,r,x,d); 22 pushup(rt); 23 } 24 int query(int rt,int l,int r,int L,int R) 25 { 26 if (l>=L&&r<=R) 27 { 28 return c[rt]; 29 } 30 int mid=(l+r)/2,s=0; 31 if (L<=mid) s=max(s,query(rt*2,l,mid,L,R)); 32 if (R>mid) s=max(s,query(rt*2+1,mid+1,r,L,R)); 33 return s; 34 } 35 int main() 36 {int i,num=0; 37 cin>>n; 38 for (i=1;i<=n;i++) 39 { 40 scanf("%d",&a[i]); 41 num++; 42 b[num]=a[i]-i; 43 a[i]-=i; 44 } 45 sort(b+1,b+num+1); 46 sz=unique(b+1,b+num+1)-(b+1); 47 for (i=1;i<=n;i++) 48 a[i]=lower_bound(b+1,b+sz+1,a[i])-b; 49 for (i=1;i<=n;i++) 50 { 51 f[i]=query(1,1,sz,1,a[i])+1; 52 update(1,1,sz,a[i],f[i]); 53 ans=max(ans,f[i]); 54 } 55 cout<<n-ans; 56 }