[LeetCode] Unique Binary Search Trees

Given n, how many structurally unique BST's (binary search trees) that store values 1...n?

For example, Given n = 3, there are a total of 5 unique BST's.

   1         3     3      2      1
           /     /      /       
     3     2     1      1   3      2
    /     /                        
   2     1         2                 3


编程思路：（引自http://cs.lmu.edu/~ray/notes/binarytrees/）

How Many Binary Trees Are There?

There are five distinct shapes of binary trees with three nodes:

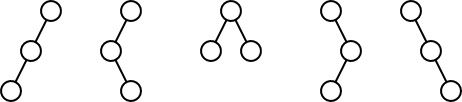
But how many are there for n nodes?

Let C(n) be the number of distinct binary trees with n nodes.  This is equal to the number of trees that have a root, a left subtree with j nodes, and a right subtree of (n-1)-j nodes, for each j.  That is,

    C(n) = C(0)C(n-1) + C(1)C(n-2) + ... + C(n-1)C(0)

which is

The first few terms:

    C(0) = 1
    C(1) = C(0)C(0) = 1
    C(2) = C(0)C(1) + C(1)C(0) = 2
    C(3) = C(0)C(2) + C(1)C(1) + C(2)C(0) = 5
    C(4) = C(0)C(3) + C(1)C(2) + C(2)C(1) + C(3)C(0) = 14
根据上面的解释，编程思路即只需决定有几个左孩子，几个右孩子就可以了。因为左右孩子数决定了，那么对于二叉搜索树来说它的根节点是唯一的。

class Solution {
public:
    int numTrees(int n) {
        vector<int> res(n+1,1);  //给所有值都赋1，则res[0]=1,res[1]=1,就不用另外写了
        
        if(n<2 && n>=0)
           return res[n]; 
        
        for(int i = 2;i<=n;i++){  //用vector<int> res记录n的大小从0到n的所有结果，这样就避免了用递归的方法。
                                   //这也是DP（动态规划）的精华所在
           res[i] = 0;
           for(int j=0;j<=i-1;j++)
              res[i] += res[j]*res[i-1-j];
        }//end for
      
        return res[n];
    }
};