AC自动机
前(che)言(dan)
Aho-Corasick automation,该算法在1975年产生于贝尔实验室,是著名的多模匹配算法之一。一个常见的例子就是给出 (n) 个单词,再给出一段包含 (m) 个字符的文章,让你找出有多少个单词在文章里出现过。要搞懂AC自动机,先得有模式树(字典树)(Trie) 和 (KMP) 模式匹配算法的基础知识。
Trie
这里的Trie可不是什么权值线段树
就是常说的字典树。
这个东西似乎很简单?不会的出门左转问度娘
一个性质是两个串的(LCP)就是这两个串对应结束位置的(LCA)
简述
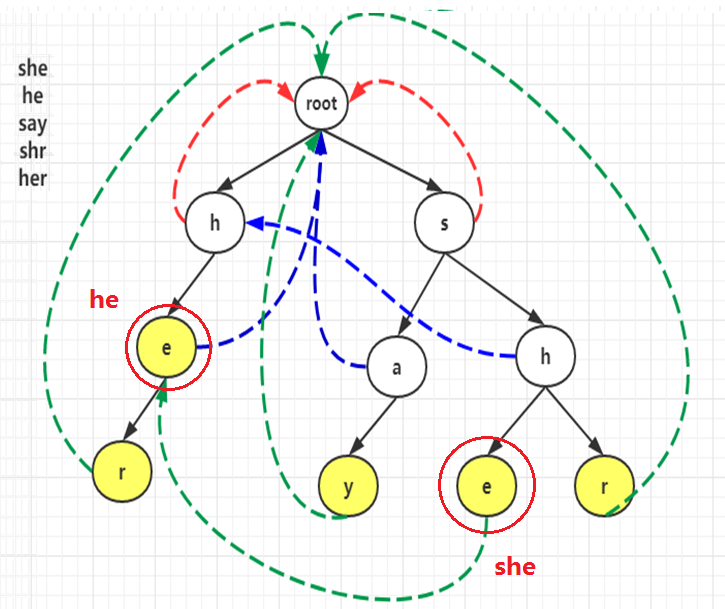 (此图蒯自网络)(右上方的几个字符串是模式串)
(此图蒯自网络)(右上方的几个字符串是模式串)
这就是一个(AC)自动机。
想要知道自动机是什么的大佬请问度娘
它大体上就是一个 (Tire) 树(Trie树中字符应该在边上,但这里字符在点上不引响解释),不过多了一些奇怪的东西,也就是图中的虚箭头。
这叫做fail指针。(Trie) 树中一个点的 (fail) 指针指向这个点代表字符串的最长后缀对应的节点。 (fail) 指针体现了 (KMP) 的思想
可以结合上面的图理解。
性质
我们发现如果我们沿着一个点的 (fail) 边一直跳,就可以遍历这个点代表字符串的所有后缀。用AC自动机解决的经典问题:多模式串匹配,就使用了AC自动机的这个性质。
我们发现 (fail) 边构成了一棵树(之后叫做fail 树),其中一个点的子树中所有的点代表的串都包含这个点代表的串(或者说这个点代表的串是这个点的 fail 树上子树中的点代表的串的子串)。 51nod 麦克打电话这个题就运用了AC自动机的这个性质。
构造
接下来讲讲如何构造(AC)自动机。
(AC)自动机就是(Trie)树上多了一些(fail)边,当然要先建出(Trie)树。
void insert(char *s){
int l=strlen(s+1);
int now=0;
for(int i=1;i<=l;i++){
if(ac[now].nxt[s[i]-'a']==0)ac[now].nxt[s[i]-'a']=++tot;
now=ac[now].nxt[s[i]-'a'];
}
ac[now].cnt++;
}
(PS:代码中ac[u].nxt[i]代表 (Trie) 树中 (u) 节点沿 (i) 字符这条边走到达的节点,ac[u].cnt代表 (Trie) 树中以 (u) 为结束为止的字符串数量)
然后就是如何建 (fail) 边了。
考虑按长度递增的顺序(例如 (bfs) 序)依次求每个节点的(fail)。假设节点 (x) 的父边上的字符是 (c),那么我们就从(fail[fa[x]]) 开始沿着 (fail) 链往上跳,直到跳到一个节点 (y) 使得 (y) 有字符为 (c) 的出边,那么这条出边走到的儿子就是 (fail[x])。
void get_fail(){
queue<int> q;
for(int i=0;i<=25;i++)
if(ac[0].nxt[i])q.push(ac[0].nxt[i]);
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=0;i<=25;i++)
if(ac[u].nxt[i]){
q.push(ac[u].nxt[i]);
int now=ac[u].fail;
while(now&&ac[now].nxt[i]==0)now=ac[now].fail;
if(now==0&&ac[now].nxt[i]==0)ac[ac[u].nxt[i]].fail=0;
else ac[ac[u].nxt[i]].fail=ac[now].nxt[i];
}
}
}
(PS:代码中ac[u].fail代表 (u) 点的 (fail) 边指向节点。
构造的复杂度分析
考虑对于属于同个串的节点建 (fail) 的总复杂度,(KMP) 用的分析依然适用,因此时间复杂度为总串长。
模板
以这道模板题为例
把文本串在 (Trie) 上进行匹配,新加一个字符时,若当前节点没有这个字符的出边,就一直沿着 (fail) 往上跳,直到跳到一个有该字符的出边为止,然后走到出边指向的儿子。然后把节点记录的结束位置个数统计一下就好了。
查询时间复杂度为文本串长度。复杂度分析同 (KMP) 复杂度分析
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<queue>
using namespace std;
const int N=1001000;
int n,ans,tot;
char s[N];
struct AC{
int nxt[26],cnt,fail;
}ac[N];
void insert(char *s){
int l=strlen(s+1);
int now=0;
for(int i=1;i<=l;i++){
if(ac[now].nxt[s[i]-'a']==0)ac[now].nxt[s[i]-'a']=++tot;
now=ac[now].nxt[s[i]-'a'];
}
ac[now].cnt++;
}
void get_fail(){
queue<int> q;
for(int i=0;i<=25;i++)
if(ac[0].nxt[i])q.push(ac[0].nxt[i]);
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=0;i<=25;i++)
if(ac[u].nxt[i]){
q.push(ac[u].nxt[i]);
int now=ac[u].fail;
while(now&&ac[now].nxt[i]==0)now=ac[now].fail;
if(now==0&&ac[now].nxt[i]==0)ac[ac[u].nxt[i]].fail=0;
else ac[ac[u].nxt[i]].fail=ac[now].nxt[i];
}
}
}
void work(char *s){
int l=strlen(s+1);
int now=0;
for(int i=1;i<=l;i++){
while(now&&ac[now].nxt[s[i]-'a']==0)now=ac[now].fail;
now=ac[now].nxt[s[i]-'a'];
for(int y=now;ac[y].cnt!=-1;y=ac[y].fail){
ans+=ac[y].cnt;
ac[y].cnt=-1;
}
}
}
int read(){
int sum=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){sum=sum*10+ch-'0';ch=getchar();}
return sum*f;
}
int main(){
n=read();
for(int i=1;i<=n;i++){
scanf("%s",s+1);
insert(s);
}
get_fail();
scanf("%s",s+1);
work(s);
printf("%d",ans);
return 0;
}
Trie图优化
假如节点 (x) 没有字符 (c) 的出边,那么不妨找到 (x) 在 (fail) 树上最近的一个有字符 (c) 出边的祖先,从 (x) 连一条边到这个点的字符 (c) 的儿子。这些边以及原本 (Trie) 树的结构构成的转移图称为 (Trie) 图。下面记 (trans[x][c]) 表示从节点 (x) 连出的字符 (c) 的出边指向的节点。
Trie 图则是相当于把 NFA 转化为了 DFA(这涉及到了自动机的概念,不了解也不影响对本篇文章的阅读,有能力的可以了解一下,可以加深理解还可以用来装逼)
建图的时候,(fail[x]) 就是 (trans[fail[fa[x]]][c])。如果 (x) 本身有字符 (c) 的儿子,那么 (trans[x][c]) 就是这个儿子,否则(trans[x][c]) = (trans[fail[x]][c])。
时间复杂度 (O(|T||∑|)),其中 (|T|) 表示 (Trie) 的大小,(|∑|)表示字符集大小。
下面是Trie图优化的代码,还是刚才那个模板题
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<queue>
using namespace std;
const int N=1001000;
int n,ans,tot;
char s[N];
struct AC{
int nxt[26],cnt,fail;
}ac[N];
void insert(char *s){
int l=strlen(s+1);
int now=0;
for(int i=1;i<=l;i++){
if(ac[now].nxt[s[i]-'a']==0)ac[now].nxt[s[i]-'a']=++tot;
now=ac[now].nxt[s[i]-'a'];
}
ac[now].cnt++;
}
void get_fail(){
queue<int> q;
for(int i=0;i<=25;i++)
if(ac[0].nxt[i])q.push(ac[0].nxt[i]);
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=0;i<=25;i++)
if(ac[u].nxt[i])q.push(ac[u].nxt[i]),ac[ac[u].nxt[i]].fail=ac[ac[u].fail].nxt[i];
else ac[u].nxt[i]=ac[ac[u].fail].nxt[i];
}
}
void work(char *s){
int l=strlen(s+1);
int now=0;
for(int i=1;i<=l;i++){
now=ac[now].nxt[s[i]-'a'];
for(int y=now;ac[y].cnt!=-1;y=ac[y].fail){
ans+=ac[y].cnt;
ac[y].cnt=-1;
}
}
}
int read(){
int sum=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){sum=sum*10+ch-'0';ch=getchar();}
return sum*f;
}
int main(){
n=read();
for(int i=1;i<=n;i++){
scanf("%s",s+1);
insert(s);
}
get_fail();
scanf("%s",s+1);
work(s);
printf("%d",ans);
return 0;
}
本文只是讲解算法,真正掌握它还需要多刷题。
完结撒花