LeetCode第[78]题(Java)：Subsets（求子集）扩展——第[90]题：Subsets 2

题目：矩阵置0

难度：Easy

题目内容：

 

Given a set of distinct integers, nums, return all possible subsets (the power set).

Note: The solution set must not contain duplicate subsets.

翻译：

给定一组不同的整数，nums，返回所有可能的子集（包括空集和自身）。

注意：解决方案集不能包含重复的子集。

Example:

Input: nums = [1,2,3]
Output:
[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

我的思路：无。。。。。

答案代码：

public List<List<Integer>> subsetsWithDup(int[] nums) {
    List<List<Integer>> list = new ArrayList<>();
    Arrays.sort(nums);
    backtrack(list, new ArrayList<>(), nums, 0);
    return list;
}

private void backtrack(List<List<Integer>> list, List<Integer> tempList, int [] nums, int start){
    list.add(new ArrayList<>(tempList));
    for(int i = start; i < nums.length; i++){
        tempList.add(nums[i]);
        backtrack(list, tempList, nums, i + 1);
        tempList.remove(tempList.size() - 1);
    }
} 

答案复杂度：O（n²）

答案思路：

其实就是利用回溯递归的思想，单独写一个回溯方法，对每一个子集都是由各个字母开头组成的（子集的子集的子集。。。）这样一个集合，

所以方法内只需要先将tempList加入结果集List，然后写一个循环，将从start开始，依次将当前nums[ i ] 加入tempList，然后递归调用回溯方法（start= i+1），调用完毕后说明以nums[ i ]开头的子集结束，所以将nums[ i ]从tempList中移出。

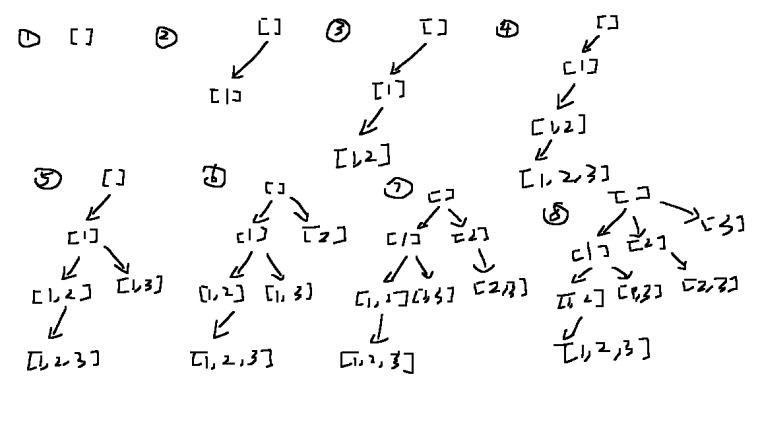
下面是流程：以输入【1，2，3】为例（在回溯方法第一行打印tempList即可看见）

[]———————从空开始
[1]——————以空开头的第一个
[1, 2]——————以1开头的第一个
[1, 2, 3]——————以12开头的第一个，此时到3了，说明以12开头的子集结束，删掉2，此时回溯到以1开头
[1, 3]——————以1开头的第二个，此时又到3，以1开头的子集结束，删掉1，回溯到以空开头
[2]——————以空开头的第二个
[2, 3]——————以2开头的第一个，此时到3，以2开头的子集结束，删掉2，回溯到以空开头
[3]——————以空开头的最后一个

扩展：当nums包含重复字符的时候应该怎么办？第[90]题：Subsets 2

1、一开始是乱序的所以需要将nums排序才能判断是否重复。

2、在回溯方法的循环里第一行加入重复判断，如果当前元素（非第一个）和上一个元素一样，那么就跳过此元素不使用递归。

public List<List<Integer>> subsetsWithDup(int[] nums) {
    List<List<Integer>> list = new ArrayList<>();
    Arrays.sort(nums);
    backtrack(list, new ArrayList<>(), nums, 0);
    return list;
}

private void backtrack(List<List<Integer>> list, List<Integer> tempList, int [] nums, int start){
    list.add(new ArrayList<>(tempList));
    for(int i = start; i < nums.length; i++){
        if(i > start && nums[i] == nums[i-1]) continue; // skip duplicates
        tempList.add(nums[i]);
        backtrack(list, tempList, nums, i + 1);
        tempList.remove(tempList.size() - 1);
    }
}