一、一维前缀和
前提:给一个长度为n的数列,m次询问,问[L,R]区间内数列各项和
1 a[0]=0; 2 for(int i=1;i<=n;i++)a[i]+=a[i-1];
所以,前缀和就是前面i个数的总和,所求区间和即为a[R]-a[L-1]
二、一维差分
前提:给一个长度为n的数列,对[L,R]区间加上或减去某个值,最后问[L,R]区间内数列各项和
1 #include<bits/stdc++.h> 2 #define mem(a) memset(a,0,sizeof(a)) 3 #define ll long long 4 #define inf 0x3f3f3f3f 5 const int N=1e6+5; 6 using namespace std; 7 int main(){ 8 int n,m,a[100],b[100]; 9 cin>>n>>m; 10 for(int i=1;i<=n;i++){ 11 cin>>a[i]; 12 } 13 for(int i=1;i<=m;i++){ 14 int l,r,t,p; 15 cin>>t>>l>>r>>p; 16 if(t==1){ 17 b[l]+=p; 18 b[r+1]-=p;//只考虑[l,r]范围 19 } 20 } 21 int add=0; 22 for(int i=1;i<=n;i++){ 23 add+=b[i]; 24 a[i]+=a[i-1]+add; 25 } 26 int L,R; 27 cin>>L>>R; 28 cout<<a[R]-a[L-1]<<endl; 29 return 0; 30 }
三、二维前缀和
前提:给定一个n*m大小的矩阵a,有q次询问,每次询问给定x1,y1,x2,y2四个数,求以(x1,y1)为左上角坐标和(x2,y2)为右下角坐标的子矩阵的所有元素和。//包含边界
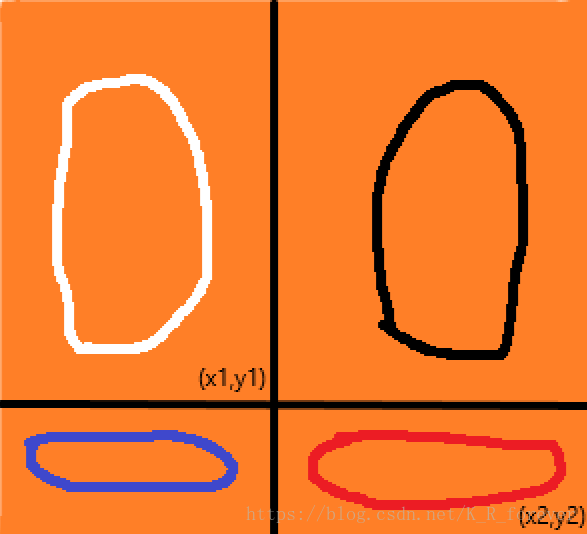
ans=a[x2][y2]-a[x1-1][y2]-a[x2][y1-1]+a[x1-1][y1-1]
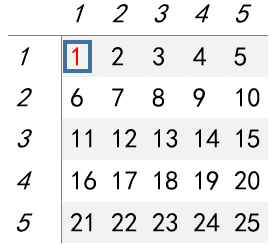
a[i][j]+=a[i][j-1]+a[i-1][j]-a[i-1][j-1]
1 #include<bits/stdc++.h>
2 #define mem(a) memset(a,0,sizeof(a))
3 #define ll long long
4 #define inf 0x3f3f3f3f
5 const int N=1e6+5;
6 using namespace std;
7 int main(){
8 int n,m,a[N][N],q;
9 cin>>n>>m>>q;
10 for(int i=1;i<=n;i++){
11 for(int j=1;j<=m;j++)
12 cin>>a[i][j];
13 }
14 for(int i=1;i<=n;i++){
15 for(int j=1;j<=m;j++)
16 a[i][j]+=a[i][j-1]+a[i-1][j]-a[i-1][j-1];
17 }
18 for(int i=1;i<=q;i++){
19 int x1,y1,x2,y2;
20 cin>>x1>>y1>>x2>>y2;
21 cout<<a[x2][y2]-a[x1-1][y2]-a[x2][y1-1]+a[x1-1][y1-1]<<endl;
22 }
23 return 0;
24 }
四、二维差分

在左上区域+5,则影响其他三个区域,所以左下右上只要-5就和原来一样,右下需+5;
b[x1][y1]+=5; b[x1][y2+1]-=5; b[x2+1][y1]-=5; b[x2+1][y2+1]+=5;