2019.4.27

1.数组中，元素的位置称为索引

2.递归，调用栈。

发现还是不会写hanoi。。：

#include<bits/stdc++.h>
using namespace std;
void hanoi(int n,char a,char b,char c){
 if(n==1) cout<<n<<":"<<a<<"-->"<<c<<endl;
 else {
    hanoi(n-1,a,c,b);
    cout<<n<<":"<<a<<"-->"<<c<<endl;
    hanoi(n-1,b,a,c);
 }
}
int main()
{
    int n;
    cin>>n;
   hanoi(n,'a','b','c');

}

3.分治：

▲步骤：1）找出基线条件（尽可能简单）

               2）不断将问题分解（缩小规模），直至符合基线条件。

▲证明欧几里得算法（辗转相除法）：

https://zh.khanacademy.org/computing/computer-science/cryptography/modarithmetic/a/the-euclidean-algorithm

【   

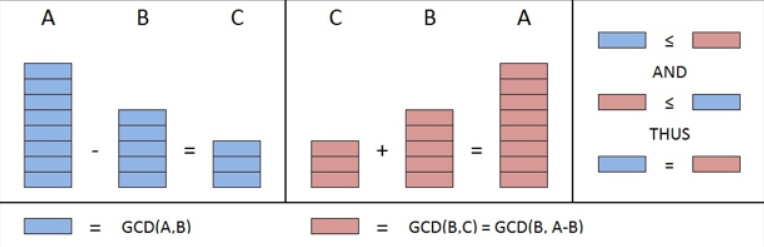
        To prove that GCD(A,B)=GCD(B,R) we first neec GCD(A,B)=GCD(B,A-B).

        Proof that the GCD(A,B) evenly dividesC .

        Proof that the GCD(B,C) evenly dividesA

        GCD(A,B)=GCD(B,A-B) 

        GCD(A,B)=GCD(A-B,B)=GCD(A-2B,B)

        GCD(A,B)=GCD(B,R)

  

】

▲排序（以下都按从小到大）：

1）冒泡排序：从左到右，数组中相邻的两个元素进行比较，将较大的放到后面。 // O(n^2)

2）选择排序：从左到右，一个元素与他下面所有元素比较，找出最小的，和那个元素互换，开始下一轮。  // O(n^2)

3）快排：找基准数，左右两边放小于等于和大于，再递归。

#include<bits/stdc++.h>
using namespace std;
void quicksort(vector<int> &num,int l,int r)
{

 if(l>= r) return;
 int i=l,j=r,x=num[l];
 while(i<j){
    while(i<j&&num[j]>=x)
        j--;
    if(i<j)
        num[i++]=num[j]; //填坑之后再加
    while(i<j&&num[i]<=x)
        i++;
    if(i<j)
        num[j--]=num[i];
 }
 num[i]=x;  //把基准值放到i处
 quicksort(num,l,i-1);  //以i为中间值，排左右两边
 quicksort(num,i+1,r);
}
int main()
{
   int f[]={3,35,2,1,8,5,6,2,0};
   int len=sizeof(f)/sizeof(int);
  /*前者是该int数组所占的内存总量（字节数),后者是单个int所占的内存,
    合起来就是数组中元素的个数*/
   vector<int> num(f,f+len);
   for(int k=0;k<num.size();k++)
    cout<<num[k]<<" ";
   cout<<endl;
   quicksort(num,0,len-1);
   for(int k=0;k<num.size();k++)
    cout<<num[k]<<" ";
   cout<<endl;
   return 0;

}