LeetCode42-接雨水

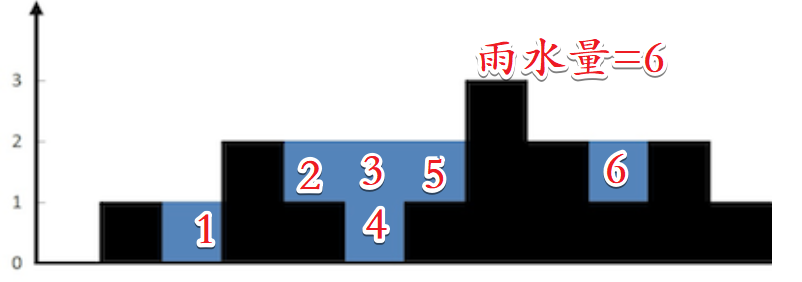
题目描述

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

我的题解

关键在于找到全部可以装雨水的'槽'
从第一个柱子开始，寻找第一个比它高的，即可组成一个槽。
如果没有更高的，就找到后面最高的，这时也可以组成一个槽

    //99.98%
    public int trap(int[] height) {
        int len = height.length;
        int rainCount = 0;//雨量
        for (int i=0;i<len-1;i++){
            if (height[i+1]>height[i])continue;//如果这个柱子比下一个低，跳过。
            int highter = height[i];//后面更高的柱子高度
            int highterIndex = i;//后面更高的柱子索引
            int max = height[i+1];//后面的最高柱子
            int maxIndex = i+1;//后面的最高柱子索引
            boolean hasHighter = false;//后面是否存在比当前柱子更高的柱子
            for (int j=i+1;j<len;j++){
                if (height[j]>=highter){//找到不低于当前柱子的柱子
                    highterIndex = j;
                    hasHighter = true;
                    break;
                }
                if (height[j]>max){//计算后面最高的
                    max = height[j];
                    maxIndex = j;
                }
            }
            if (!hasHighter) {//如果后面没有更高的柱子，就是用后面的最高柱子
                highterIndex = maxIndex;
                highter = max;
            }
            for (int j=i+1;j<highterIndex;j++){//计算这个槽可以积累的雨量
                rainCount+=highter-height[j];
            }
            i=highterIndex-1;//跳到这个槽的右边柱子
        }
        return rainCount;
    }

分析：
时间复杂度：O(N)，虽然看似有来两个循环，但是他们是线性的
空间复杂度: O(1),只使用了几个变量而已

其他解法

单调栈

public class Solution {
    public int trap(int[] height) {
        if (height == null) {
            return 0;
        }
        Stack<Integer> stack = new Stack<>();
        int ans = 0;
        for (int i = 0; i < height.length; i++) {
            while(!stack.isEmpty() && height[stack.peek()] < height[i]) {
                int curIdx = stack.pop();
                // 如果栈顶元素一直相等，那么全都pop出去，只留第一个。
                while (!stack.isEmpty() && height[stack.peek()] == height[curIdx]) {
                    stack.pop();
                }
                if (!stack.isEmpty()) {
                    int stackTop = stack.peek();
                    // stackTop此时指向的是此次接住的雨水的左边界的位置。右边界是当前的柱体，即i。
                    // Math.min(height[stackTop], height[i]) 是左右柱子高度的min，减去height[curIdx]就是雨水的高度。
                    // i - stackTop - 1 是雨水的宽度。
                    ans += (Math.min(height[stackTop], height[i]) - height[curIdx]) * (i - stackTop - 1);
                }
            }
            stack.add(i);
        }
        return ans;
    }
}