Description
iSea is tired of writing the story of Harry Potter, so, lucky you, solving the following problem is enough.
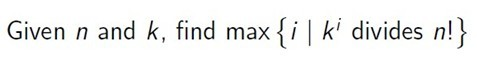
Input
The first line contains a single integer T, indicating the number of test cases.
Each test case contains two integers, N and K.
Technical Specification
- 1 <= T <= 500
- 1 <= K <= 1 000 000 000 000 00
- 1 <= N <= 1 000 000 000 000 000 000
Output
For each test case, output the case number first, then the answer, if the answer is bigger than 9 223 372 036 854 775 807, output “inf” (without quote).
Sample Input
2
2 2
10 10
Sample Output
Case 1: 1
Case 2: 2
这题直接上定理吧……
勒让德定理:在(n!)的素因子分解式中,素数(p)的指数记为(L_p(n!)),则(L_p(n!)=sumlimits_{k=1}lfloorfrac{n}{p^k} floor)
证明如下:
将(1,2,3,...,n)都分解为标准形式,记其中(p)的指数为(r)的有(m_r)个((rgeqslant 1)),则(L_p(n!)=m_1+2m_2+...=sumlimits_{i=1}im_i)
分组可得(L_p(n!)=sumlimits_{i=1}m_i+sumlimits_{i=2}m_i+...),令(N_r=sumlimits_{i=r}m_i),则(L_p(n!)=sumlimits_{i=1}N_i)
易得(N_r=sumlimits_{i=r}m_i)恰好是这(n)个数中能整除(p^r)的数的个数,故(N_r)=(lfloorfrac{n}{p^r} floor),故该定理得证
/*program from Wolfycz*/
#include<map>
#include<cmath>
#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
#define Fi first
#define Se second
#define ll_inf 1e18
#define MK make_pair
#define sqr(x) ((x)*(x))
#define pii pair<int,int>
#define int_inf 0x7f7f7f7f
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
inline char gc(){
static char buf[1000000],*p1=buf,*p2=buf;
return p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++;
}
template<typename T>inline T frd(T x){
int f=1; char ch=gc();
for (;ch<'0'||ch>'9';ch=gc()) if (ch=='-') f=-1;
for (;ch>='0'&&ch<='9';ch=gc()) x=(x<<1)+(x<<3)+ch-'0';
return x*f;
}
template<typename T>inline T read(T x){
int f=1; char ch=getchar();
for (;ch<'0'||ch>'9';ch=getchar()) if (ch=='-') f=-1;
for (;ch>='0'&&ch<='9';ch=getchar()) x=(x<<1)+(x<<3)+ch-'0';
return x*f;
}
inline void print(int x){
if (x<0) putchar('-'),x=-x;
if (x>9) print(x/10);
putchar(x%10+'0');
}
const int N=1e7;
int prime[N+10],tot;
bool inprime[N+10];
void prepare(){
for (int i=2;i<=N;i++){
if (!inprime[i]) prime[++tot]=i;
for (int j=1;j<=tot&&i*prime[j]<=N;j++){
inprime[i*prime[j]]=1;
if (i%prime[j]==0) break;
}
}
}
int main(){
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
prepare();
int T=read(0);
for (int Case=1;Case<=T;Case++){
ll n=read(0ll),k=read(0ll),Ans=ll_inf;
printf("Case %d: ",Case);
if (k==1){
printf("inf
");
continue;
}
for (int i=1;i<=tot;i++){
if (k%prime[i]) continue;
ll cntk=0,cntn=0,_n=n;
while (k%prime[i]==0) k/=prime[i],cntk++;
while (_n/=prime[i]) cntn+=_n;
Ans=min(Ans,cntn/cntk);
if (k==1) break;
}
if (k>1){
ll _n=n,cntn=0;
while (_n/=k) cntn+=_n;
Ans=min(Ans,cntn);
}
printf("%lld
",Ans);
}
return 0;
}