E. Sergey's problem
【题目描述】
给出一个n个点m条边的有向图,需要找到一个集合使得1、集合中的各点之间无无边相连2、集合外的点到集合内的点的最小距离小于等于2。
【算法】
官方题解证明的很强。对任意一个点 a(未访问过)删去其所有子节点,若剩余点组成的新图的答案集合不存在到 a 的边,则将 a 加入答案集合中;否则 删去a。一遍正向对 1~n 的每一个点遍历,保留父节点打上标记 -1,子节点打上标记 1。下一步就是删去不满足条件的点,对任意一个标有 -1 的点 i,首先应该找到剩余点的答案集合(即从 i+1 到 n 的所有满足条件的点),于是我们可以考虑从 n ~ 1 逆向遍历,这样即可满足条件。
给出一个反例(不太会用graphviz,逃。。。。):
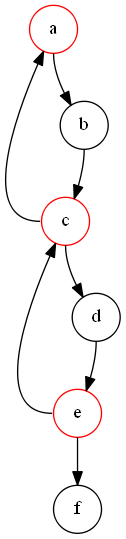
如果正向删的话,只留下了e点显然gg。
【代码】
#include <bits/stdc++.h>
#define N 1000100
using namespace std;
int n,m,a,b,ans;
int v[N];
vector<int> head[N];
inline int read() {
int x=0,f=1; char c=getchar();
while(c<'0'||c>'9') { if(c=='-') f=-1; c=getchar(); }
while(c>='0'&&c<='9') { x=x*10+c-'0'; c=getchar(); }
return x*f;
}
int main() {
n=read(),m=read();
for(int i=1;i<=m;i++) a=read(),b=read(),head[a].push_back(b);
for(int i=1;i<=n;i++) {
if(v[i]) continue;
int sz=head[i].size();
v[i]=-1;
for(int j=0;j<sz;j++) {
if(v[head[i][j]]) continue;
v[head[i][j]]=1;
}
}
for(int i=n;i>=1;i--) {
if(v[i]==1) continue;
ans++;
int sz=head[i].size();
for(int j=0;j<sz;j++)
v[head[i][j]]=1;
}
cout<<ans<<endl;
for(int i=1;i<=n;i++)
if(v[i]==-1) cout<<i<<" ";
return 0;
}