POJ 3525 Most Distant Point from the Sea (半平面交 + 凸多边形最大内切圆 + 二分)

题目：传送门

题意：有一个多边形的岛，岛的四周都是海，问你岛上的点到离它最近的海的距离最大是多少。

思路：

这题实际上就是求多边形的核的最大内切圆半径。

求多边形内核用半平面交即可，关键是求最大内切圆半径。

可以让多边形的每条边向里缩进 x 个单位得到新的多边形，判断其是否存在内核。

可以二分这个 x，若存在内核，移动左边界，否则，移动右边界。

考虑如何求直线向里缩进 d 个单位后的直线的表达式

我们知道直线上两点，那事情就很好办了。

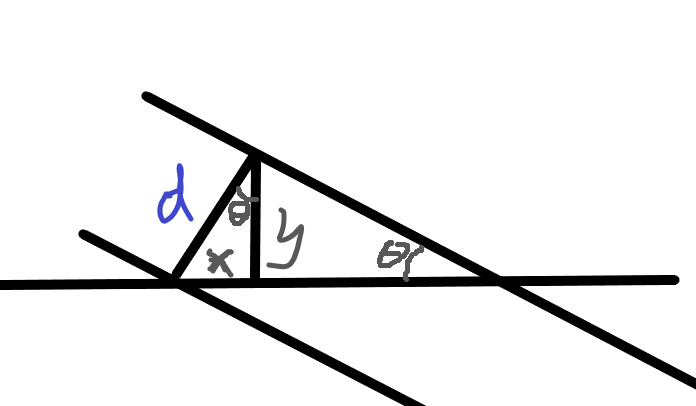
 两个点 y 的变化量 y = d * cos(θ) 

 两个点 x 的变化量 x = d * sin(θ)

然后我们已知变化前的直线的两点，我们就可以求出 cos(θ) 和 sin(θ) 了

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <queue>
#include <map>
#include <vector>
#include <set>
#include <string>
#include <math.h>

#define LL long long
#define mem(i, j) memset(i, j, sizeof(i))
#define rep(i, j, k) for(int i = j; i <= k; i++)
#define dep(i, j, k) for(int i = k; i >= j; i--)
#define pb push_back
#define make make_pair
#define INF INT_MAX
#define inf LLONG_MAX
#define PI acos(-1)
#define fir first
#define sec second
using namespace std;

const int N = 1555;
const double eps = 1e-8;

struct Point {
    double x, y;
    Point(double x = 0, double y = 0) : x(x), y(y) { }
};

Point operator + (Point A, Point B) { return Point(A.x + B.x, A.y + B.y); }
Point operator - (Point A, Point B) { return Point(A.x - B.x, A.y - B.y); }
Point operator * (Point A, double p) { return Point(A.x * p, A.y * p); }
Point operator / (Point A, double p) { return Point(A.x / p, A.y / p); }

double Cross(Point A, Point B) { return A.x * B.y - A.y * B.x; }
double Dot(Point A, Point B) { return A.x * B.x + A.y * B.y; }
double Length(Point A) { return sqrt(Dot(A, A)); }
/* 有向直线，它的左边就是对应的半平面 */
struct Line {
    Point p; /// 直线任意一点
    Point v; /// 方向向量
    double ang; /// 极角，即从x正半轴旋转到向量v所需要的角（弧度）
    Line() { }
    Line(Point p, Point v) : p(p), v(v) { ang = atan2(v.y, v.x); }
    bool operator < (const Line& L) const {
        return ang < L.ang;
    }
};

/* 点p在有向直线L的左边 */
bool OnLeft(Line L, Point p) {
    return Cross(L.v, p - L.p) >= 0;
}

/* 二直线交点，假设交点唯一存在。*/
Point GLI(Line a, Line b) {
    Point u = a.p - b.p;
    double t = Cross(b.v, u) / Cross(a.v, b.v);
    return a.p + a.v * t;
}

int HPI(Line* L, int n, Point* Q) {
    sort(L, L + n); /// 极角排序

    int st, ed; /// 双端队列的第一个元素和最后一个元素的下标

    Point *p = new Point[n]; /// p[i]为q[i]和q[i+1]的交点
    Line *q = new Line[n]; /// 双端队列
    q[st = ed = 0] = L[0];

    rep(i, 1, n - 1) {
        while(st < ed && !OnLeft(L[i], p[ed - 1])) ed--;
        while(st < ed && !OnLeft(L[i], p[st])) st++;

        q[++ed] = L[i];

        /// 平行取内测那条
        if(fabs(Cross(q[ed].v, q[ed - 1].v)) < eps) {
            ed--;
            if(OnLeft(q[ed], L[i].p)) q[ed] = L[i];
        }

        if(st < ed) p[ed - 1] = GLI(q[ed - 1], q[ed]);

    }

    while(st < ed && !OnLeft(q[st], p[ed - 1])) ed--;

    if(ed - st <= 1) return 0;

    p[ed] = GLI(q[ed], q[st]);

    int m = 0;
    rep(i, st, ed) Q[m++] = p[i];
    return m;
}

void change(Point A, Point B, Point &C, Point &D, double p) { /// 求A,B两点向里移动d距离后的两点C,D
    double len = Length(B - A);
    double addx = (A.y - B.y) * p / len;
    double addy = (B.x - A.x) * p / len;
    C.x = A.x + addx; C.y = A.y + addy;
    D.x = B.x + addx; D.y = B.y + addy;
}

Point P[N], Q[N];

Line L[N];

void solve() {
    int n;
    while(scanf("%d", &n)) {
        if(n == 0) return ;
        rep(i, 0, n - 1) scanf("%lf %lf", &P[i].x, &P[i].y);

        double l = 0.0, r = 100000.0, ans = 0.0;
        while(r - l >= eps) {
            double mid = (l + r) / 2.0;
            rep(i, 0, n - 1) {
                Point A, B;
                change(P[i], P[(i + 1) % n], A, B, mid);
                L[i] = Line(A, B - A);
            }

            int flag = HPI(L, n, Q);
            if(flag == 0) r = mid - eps;
            else {
                ans = mid;
                l = mid + eps;
            }
        }

        printf("%.6f
", ans);

    }
}

int main() {

//    int _; scanf("%d", &_);
//    while(_--) solve();

    solve();

    return 0;
}