罗马曲面,像是一个被捏扁的正四面体.
本文将展示罗马曲面的生成算法和切图,使用自己定义语法的脚本代码生成数学图形.相关软件参见:数学图形可视化工具,该软件免费开源.QQ交流群: 367752815
维基上关于罗马曲面的解释如下:
The Roman surface or Steiner surface (so called because Jakob Steiner was in Rome when he thought of it) is a self-intersecting mapping of the real projective plane into three-dimensional space, with an unusually high degree of symmetry. This mapping is not an immersion of the projective plane; however, the figure resulting from removing six singular points is one.
The simplest construction is as the image of a sphere centered at the origin under the map f(x,y,z) = (yz,xz,xy). This gives an implicitformula of
Also, taking a parametrization of the sphere in terms of longitude (θ) and latitude (φ), gives parametric equations for the Roman surface as follows:
- x = r2 cos θ cos φ sin φ
- y = r2 sin θ cos φ sin φ
- z = r2 cos θ sin θ cos2 φ.
罗马曲面脚本代码:
#http://www.ipfw.edu/departments/coas/depts/math/coffman/steinersurface.html #Steiner's Roman Surface. Three double lines, six pinch points, and a triple point. #plot3d([r^2*sin(t)*cos(t), r*sin(t)*(1-r^2)^(1/2), r*cos(t)*(1-r^2)^(1/2)], r=0..1, t=0..2*Pi, numpoints=2500) vertices = D1:160 D2:80 u = from 0 to (PI) D1 v = from 0 to (PI) D2 a = sin(u) b = cos(u) c = sin(v) d = cos(v) r = 5.0 x = r*r*b*d*c y = r*r*a*d*c z = r*r*b*a*d*d

我还找到几个与罗马曲面相关的图形
The three double lines of Steiner's Roman Surface coincide
vertices = D1:100 D2:100 t = from 0 to (PI*2) D1 r = from 0 to 1 D2 y = 1-r^2+(r^2)*(sin(t)^2) x = (r^2)*(sin(t)^2) + 2*(r^2)*sin(t)*cos(t) z = sqrt((1-r^2)/2) * r * (sin(t)+cos(t)) x = x*5 y = y*5 z = z*5
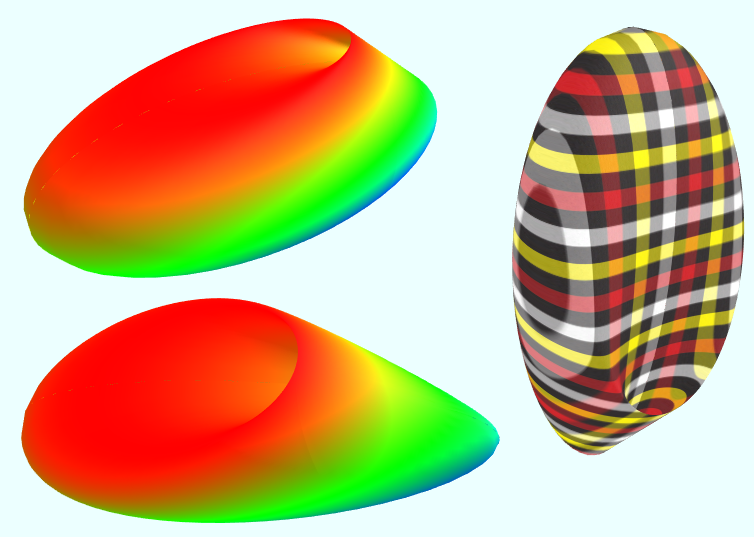
Two of the three double lines in Steiner's Roman Surface
vertices = D1:100 D2:100 t = from 0 to (PI*2) D1 r = from 0 to 1 D2 x = 2*r*cos(t)*sqrt(1-r^2) y = 2*r*sin(t)*sqrt(1-r^2) z = 1-2*r*r*(cos(t)^2) x = x*5 y = y*5 z = z*5

