K*邻法
K-*邻模型
根据一个已经分好类具有具体标签的数据集进行预测分类,不具有显示的训练过程,根据新样本与训练样本中每个样本之间的距离选择最*的K个样本预测,通过多数投票的方式预测该样本的标签。
模型由三个基本要素组成:距离度量,K值选择,分类决策规则。该模型距离度量为欧式距离,分类决策规则是多数投票表决。
距离度量
Lp(x1,x2) = (sum(|x1-x2|p))1/p
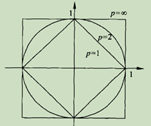
当p = 1时,称为曼哈顿距离,L1(x1,x2) = (sum(|x1-x2|)) 各个维度差值绝对值之和。
当p = 2时,称为欧式距离,L2(x1,x2) = (sum(|x1-x2|2))1/2 各个维度差值平方之和再开方。
当p = oo时,它是各个坐标的最大值,L2(x1,x2) =max(|x1-x2|) 维度差值最大的绝对值。
各种距离原点为1的点
K值的选择
K值的选择对于k*邻算法会产生很大的影响。
如果k值的选择较小,相当于在较小邻域内进行预测,学*的*似误差会减小,只有与输入实例较*的训练示例才会有很好的预测结果。但是学*的估计误差会增大,预测结果会与*邻实例点很敏感,如果正巧*邻实例点是噪声,预测将会出错,容易发生过拟合。
如果K值较大,相当于在较大邻域内进行预测,学*的*似误差会增大,距离较远的实例点可能对预测产生影响,模型比较简单。但是学*的估计误差会减少。
在实际应用中,一般选择较小的K值,通过交叉验证法选取最合适的K值。
分类决策规则
K*邻模型一般选择多数表决,即输入实例的最*的k个实例最大的类。
kd树
k*邻最简单的实现方法是线性扫描,计算输入点与所有样本点的距离。计算效率较低,当维数较高时,通常构建kd树,减少计算距离的次数。
Kd树是一种k维实例点进行存储并快速搜索的树形数据结构。是一种二叉树,相当于不断用垂直于坐标轴的超平面对k维空间进行切割,构成一系列超矩形区域。每个结点对应一个超矩形区域。
构建kd树
选取每个维度中位数作为切分,这样得到的kd是平衡二叉树,但效率未必最优。
例1
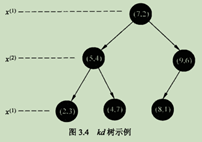
给定一个二维空间数据集T={(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)},构造一颗平衡二叉树。
首先根据第一维度7切分,(7,2)划分。接着左矩阵以第二维度4划分(5,4),右矩阵与第二维度6切分,以此递归类推。只看没有在边界线上的点。

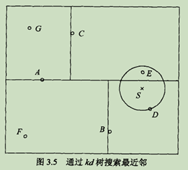
搜索kd树
算法
(1) 在kd树中找到包含目标点x的叶子结点。
(2) 以此子叶结点为最*临*点。
(3) 递归向上,如果父结点距离更*,则以此结点为最邻*点,检查父结点另一结点区域的点是否有更短的距离。以目标点为球心,目标点与临*点的距离为半径画超球体。如果与另一区域相交,在另一区域可能存在最*临*点,递归查找,否则向上回退
(4) 回退到根节点。搜索结束。
例2