数学图形(2.3)绕在圆环上的曲线

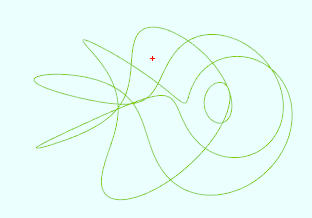
圆环面螺线

#http://xuxzmail.blog.163.com/blog/static/25131916200976114621705/
#Toroidal spiral

vertices = 1000

t = from 0 to (2*PI)

r = 5
n = 20

x = (r+sin(20*t))*cos(t)
y = (r+sin(20*t))*sin(t)
z = cos(n*t)

r = 10;
x = x*r
y = y*r
z = z*r

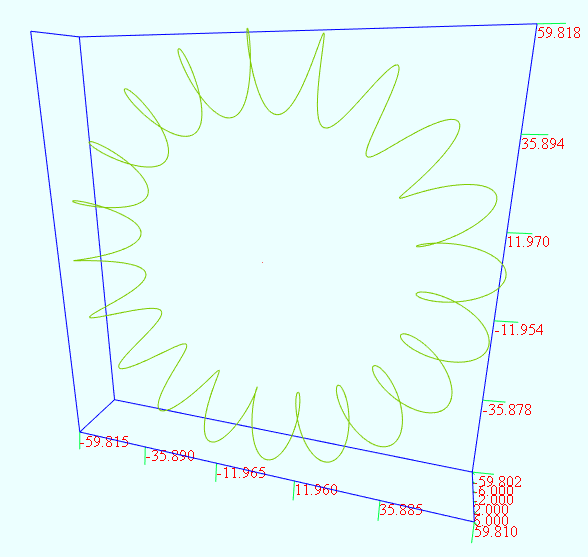
在前面讲了N叶结,当N值越大时,你会发现整个图形越像一个圆环.这一节就讲其他几种绕在圆环上的曲线.

vertices = 12000
t = from 0 to (64*PI)

p = rand_int2(2, 32)
q = rand_int2(2, 32)

r = 2 + cos(q/p*t)

x = r*sin(t)
y = sin(q/p*t)
z = r*cos(t)

r = 0.5 + 0.5*sin(t)
g = 0.5 + 0.5*y
b = 0.5 + 0.5*cos(t)

另一个圆环上的曲线

#http://www.mathcurve.com/courbes3d/solenoidtoric/solenoidtoric.shtml

vertices = 10000

t = from 0 to (20*PI)

n = rand2(0.5, 10)
a = rand2(5, 10)
b = rand2(1, 5)

x = (a + b*cos(n*t))*cos(t)
z = (a + b*cos(n*t))*sin(t)
y = b*sin(n*t)

knot(37)

vertices = 10000
t = from 0 to (6*PI)

p = 3
q = 7

r = 2 + cos(q/p*t)

x = r*sin(t)
y = sin(q/p*t)
z = r*cos(t)

r = 0.5 + 0.5*sin(t)
g = 0.5 + 0.5*y
b = 0.5 + 0.5*cos(t)