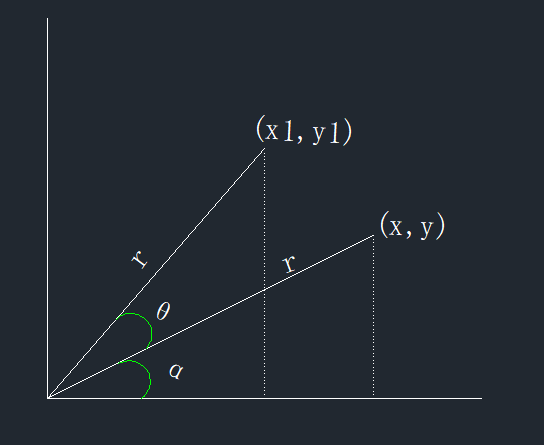
上图将向量(x,y)旋转到((x_1,y_1)),求旋转矩阵。即已知角度( heta),问题表述为矩阵方程:
[egin{bmatrix}
x_1 \
y_1
end{bmatrix}
=
A*
egin{bmatrix}
x \
y
end{bmatrix}
]
求变换矩阵(A)。
方法一
利用平面几何的方法。
[egin{split}
x_1 = {}&cos( heta+alpha)*r\
= {}&cos( heta)*cos(alpha)*r - sin( heta)*sin(alpha)*r\
= {}& cos( heta)*x-sin( heta)*y
end{split}
]
[egin{split}
y_1 = {}&sin( heta+alpha)*r\
= {}&sin( heta)*cos(alpha)*r+cos( heta)*sin(alpha)*r\
= {}&sin( heta)*x + cos( heta)*y
end{split}
]
这个线性方程组写成矩阵形式,可得
[A =
egin{bmatrix}
cos( heta) & -sin( heta)\
sin( heta) & cos( heta)
end{bmatrix}
]
方法二
利用线性变换的方法
(R^2)中的任意一点(x,y)经过旋转( heta)后变为(x1,y1),求旋转矩阵。
这是一个线性变换,设变换为
[T(X) = AX
]
(X)为一个(R^2)的向量,按题意即是求变换矩阵(A)。
设(I)为(R^2)的单位矩阵,(e)为单位列向量。即:
[ I = egin{bmatrix}
1&0\
0&1
end{bmatrix}
=(e1,e2)
]
按照直角坐标系理解,e1就是x轴上的(1,0)点,e2就是y轴上的(0,1)点。
[X = x*e1 + y*e2
]
由于是线性变换,所以
[T(X) = T(x*e1 + y*e2)
= x*T(e1) + y*T(e2)
=egin{bmatrix}
T(e1)&T(e2)
end{bmatrix}*
egin{bmatrix}
x\y
end{bmatrix}
]
所以
[A =egin{bmatrix}
T(e1)&T(e2)
end{bmatrix}
]

(T(e))通过平面几何可以很容易求出来。三角形的斜边长度是1,角度是( heta),那么对边是(sin( heta)),即x坐标,邻边是(cos( heta)),即y坐标。
[ T(e1) = egin{bmatrix}
cos( heta)\
sin( heta)
end{bmatrix}
]
同理求得:
[ T(e2) = egin{bmatrix}
-sin( heta)\
cos( heta)
end{bmatrix}
]
因为旋转到x轴的负方向,所以取负值。
所以
[ A = egin{bmatrix}
cos( heta)&-sin( heta)\
sin( heta)&cos( heta)
end{bmatrix}
]