决策树
这个决策树实际上也是看了很多次,如果没有自己整理一下,推导推导,很难知其所以然,总是浅尝辄止永远不会真正地懂得。成功需要四样东西:孤独,勇气,坚持,舍弃。然而并不没有做到。废话少说,马上进入正题。
一、为什么会有决策树
决策树就是一批IF-THEN的语句,源于生活,无处不在。当人们进行选择时,就会根据事物的属性判断是好是坏,是选择还是放弃。抛开严格的数学表达,举例如下:
例1:
母亲:我朋友给你介绍个对象,明天你去约吗
女儿:帅吗
母亲:一般
女儿:有1.7m吗
母亲:1.71m
女儿:大学是985吗
母亲:是。
女儿:多重,有50kg吗
母亲:有54kg
女儿:是南方人吗
母亲:是的
女儿:好吧,约。
这是一个决策。这些决策可以用IF-THEN来表示,写成决策树那样。女儿根据母亲提供的对象属性来决定约或者不约。这样的例子无处不在。
例2:
另外,更贴切地,比如图书馆将书籍分类。分类的方法多种多样,这里假设有这两种情况:
情况一:

情况二:

抛开个人感情来判断哪种分类方式好?当然是第一种。因为搜索所需要的次数少,或者编码短。这里只是作者实在想不到更多的属性,要不然,第二种情况可能还会继续分下去,树的深度更大,编码更长。既然有各种各样的分类方式,总有好坏之分,如何使好如何使坏?众说纷纭!我们给出客观的评价:编码越短越好!也许不是信息类专业的人不喜欢编码这个概念。那就换种说法:树的深度越浅越好。这是不可争议的,是非常合理的。这样是查找书籍更加简单。从深一层来讲,每个分类都尽可能均匀一些,以使深度浅一些。
二、决策树——ID3
为了更好的分类,我们使用ID3算法。这里,ID3算法是贪婪算法,是启发式算法。根据某个指标的大小来判断用哪个属性分类。这么多属性首先用哪个?要不要全部用?
(1)指标使用信息增益
(2)设定阀值,小于阀值,算法终止,不再使用剩下的属性
(3)算法流程如下:





三、决策树——C4.5
只需要将增益换成增益比就好了。
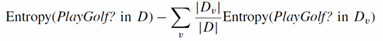


这里注意SplitInfo的计算。是避免分支的过多而是信息增益变高的做法。比如一共14个样本,分支为5,4,5。那么SplitInfo=5/14log2(14/5)*2+4/14log2(14/4).
四、剪枝
决策树为什么要剪枝?原因就是避免决策树“过拟合”样本。前面的算法生成的决策树非常的详细而庞大,每个属性都被详细地加以考虑。
法1:
基于误判的剪枝。这个思路很直接,完全的决策树不是过度拟合么,我再搞一个测试数据集来纠正它。对于完全决策树中的每一个非叶子节点的子树,我们尝试着把它替换成一个叶子节点,该叶子节点的类别我们用子树所覆盖训练样本中存在最多的那个类来代替,这样就产生了一个简化决策树,然后比较这两个决策树在测试数据集中的表现,如果简化决策树在测试数据集中的错误比较少,并且该子树里面没有包含另外一个具有类似特性的子树(所谓类似的特性,指的就是把子树替换成叶子节点后,其测试数据集误判率降低的特性),那么该子树就可以替换成叶子节点。该算法以bottom-up的方式遍历所有的子树,直至没有任何子树可以替换使得测试数据集的表现得以改进时,算法就可以终止。
法2:
第一种方法很直接,但是需要一个额外的测试数据集,能不能不要这个额外的数据集呢?为了解决这个问题,于是就提出了悲观剪枝。该方法剪枝的依据是训练样本集中的样本误判率。我们知道一颗分类树的每个节点都覆盖了一个样本集,根据算法这些被覆盖的样本集往往都有一定的误判率,因为如果节点覆盖的样本集的个数小于一定的阈值,那么这个节点就会变成叶子节点,所以叶子节点会有一定的误判率。而每个节点都会包含至少一个的叶子节点,所以每个节点也都会有一定的误判率。悲观剪枝就是递归得估算每个内部节点所覆盖样本节点的误判率。剪枝后该内部节点会变成一个叶子节点,该叶子节点的类别为原内部节点的最优叶子节点所决定。然后比较剪枝前后该节点的错误率来决定是否进行剪枝。该方法和前面提到的第一种方法思路是一致的,不同之处在于如何估计剪枝前分类树内部节点的错误率。
悲观剪枝的思路非常巧妙。把一颗子树(具有多个叶子节点)的分类用一个叶子节点来替代的话,误判率肯定是上升的(这是很显然的,同样的样本子集,如果用子树分类可以分成多个类,而用单颗叶子节点来分的话只能分成一个类,多个类肯定要准确一些)。于是我们需要把子树的误判计算加上一个经验性的惩罚因子。对于一颗叶子节点,它覆盖了N个样本,其中有E个错误,那么该叶子节点的错误率为(E+0.5)/N。这个0.5就是惩罚因子,那么一颗子树,它有L个叶子节点,那么该子树的误判率估计为。这样的话,我们可以看到一颗子树虽然具有多个子节点,但由于加上了惩罚因子,所以子树的误判率计算未必占到便宜。剪枝后内部节点变成了叶子节点,其误判个数J也需要加上一个惩罚因子,变成J+0.5。那么子树是否可以被剪枝就取决于剪枝后的错误J+0.5在
的标准误差内。
对于样本的误差率e,我们可以根据经验把它估计成各种各样的分布模型,比如是二项式分布,比如是正态分布。我们以二项式分布为例,啰嗦几句来分析一下。什么是二项分布,在n次独立重复试验中,设事件A发生的次数为X,如果每次试验中中事件A发生的概率是p,那么在n次独立重复试验中,事件A恰好发生k次的概率是
其概率期望值为np,方差为np(1-p)。比如投骰子就是典型的二项分布,投骰子10次,掷得4点的次数就服从n=10,p=1/6的二项分布。
如果二项分布中n=1时,也就是只统计一次,事件A只可能有两种取值1或0,那么事件A的值所代表的分布就是伯努利分布。B(1,p)~f(1;1,p)就是伯努利分布,伯努利分布式是二项分布的一种特殊形式。比如投硬币,正面值为1,负面值为0,那么硬币为正面的概率为p=0.5,该硬币值就服从概率为0.5的伯努利分布。
当n趋于无限大时,二项式分布就正态分布,如下图。
那么一棵树错误分类一个样本值为1,正确分类一个样本值为0,该树错误分类的概率(误判率)为e(e为分布的固有属性,可以通过统计出来),那么树的误判次数就是伯努利分布,我们可以估计出该树的误判次数均值和方差:
把子树替换成叶子节点后,该叶子的误判次数也是一个伯努利分布,其概率误判率e为(E+0.5)/N,因此叶子节点的误判次数均值为
那么,如果子树可以被叶子节点替代,它必须满足下面的条件:
这个条件就是剪枝的标准。根据置信区间,我们设定一定的显著性因子,我们可以估算出误判次数的上下界。
误判次数也可以被估计成一个正态分布,有兴趣大家可以推导一下。
连续值属性的改进
相对于那些离散值属性,分类树算法倾向于选择那些连续值属性,因为连续值属性会有更多的分支,熵增益也最大。算法需要克服这种倾向。还记得前面讲得如何克服分类树算法倾向于离散值较多的离散属性么?对了,我们利用增益率来克服这种倾向。增益率也可以用来克服连续值属性倾向。增益率作为选择属性的依据克服连续值属性倾向,这是没有问题的。但是如果利用增益率来选择连续值属性的分界点,会导致一些副作用。分界点将样本分成两个部分,这两个部分的样本个数之比也会影响增益率。根据增益率公式,我们可以发现,当分界点能够把样本分成数量相等的两个子集时(我们称此时的分界点为等分分界点),增益率的抑制会被最大化,因此等分分界点被过分抑制了。子集样本个数能够影响分界点,显然不合理。因此在决定分界点是还是采用增益这个指标,而选择属性的时候才使用增益率这个指标。这个改进能够很好得抑制连续值属性的倾向。当然还有其它方法也可以抑制这种倾向,比如MDL,有兴趣的读者可以自己阅读相关文章。
五、剪枝算法流程


参考文献:
http://blog.sina.com.cn/s/blog_68ffc7a40100urn3.html