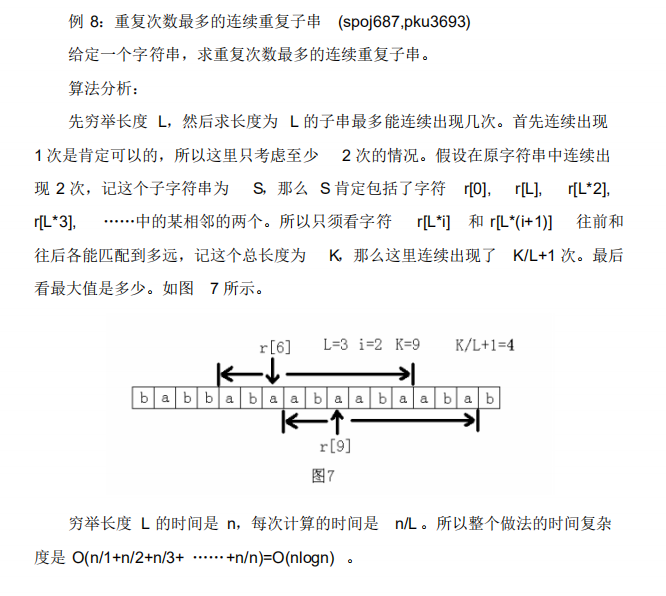
论文题例8
https://blog.csdn.net/queuelovestack/article/details/53031731这个解释很好
其实,当枚举的重复子串长度为i时,我们在枚举r[i*j]和r[i*(j+1)]的过程中,必然可以出现r[i*j]在第一个重复子串里,而r[i*(j+1)]在第二个重复子串里的这种情况,如果此时r[i*j]是第一个重复子串的首字符,这样直接用公共前缀k除以i并向下取整就可以得到最后结果。但如果r[i*j]如果不是首字符,这样算完之后结果就有可能偏小,因为r[i*j]前面可能还有少许字符也能看作是第一个重复子串里的。
于是,我们不妨先算一下,从r[i*j]开始,除匹配了k/i个重复子串,还剩余了几个字符,剩余的自然是k%i个字符。如果说r[i*j]的前面还有i-k%i个字符完成匹配的话,这样就相当于利用多余的字符还可以再匹配出一个重复子串,于是我们只要检查一下从r[i*j-(i-k%i)] (前缀首字符位置)和r[i*(j+1)-(i-k%i)]开始是否有i-k%i个字符能够完成匹配即可,也就是说去检查这两个后缀的最长公共前缀是否比i-k%i大即可。
当然如果公共前缀不比i-k%i小,自然就不比i小,因为后面的字符都是已经匹配上的,所以为了方便编写,程序里面就直接去看是否会比i小就可以了。
用了rmq区间最小来求 位置i*j的前缀 和 i*j+1位置的前缀的最长公共前缀
//为什么这样能求出重复次数最多的连续重复子串 请先搞懂next循环节求连续重复子串 这题就懂了 https://www.cnblogs.com/WTSRUVF/p/9461066.html
#include <iostream> #include <cstdio> #include <sstream> #include <cstring> #include <map> #include <cctype> #include <set> #include <vector> #include <stack> #include <queue> #include <algorithm> #include <cmath> #define rap(i, a, n) for(int i=a; i<=n; i++) #define rep(i, a, n) for(int i=a; i<n; i++) #define lap(i, a, n) for(int i=n; i>=a; i--) #define lep(i, a, n) for(int i=n; i>a; i--) #define rd(a) scanf("%d", &a) #define rlld(a) scanf("%lld", &a) #define rc(a) scanf("%c", &a) #define rs(a) scanf("%s", a) #define MOD 2018 #define LL long long #define ULL unsigned long long #define Pair pair<int, int> #define mem(a, b) memset(a, b, sizeof(a)) #define _ ios_base::sync_with_stdio(0),cin.tie(0) //freopen("1.txt", "r", stdin); using namespace std; const int maxn = 1000005, INF = 0x7fffffff; int s[maxn]; int sa[maxn], t[maxn], t2[maxn], c[maxn], n; int ran[maxn], height[maxn]; int d[50010][100]; void get_sa(int m) { int i, *x = t, *y = t2; for(i = 0; i < m; i++) c[i] = 0; for(i = 0; i < n; i++) c[x[i] = s[i]]++; for(i = 1; i < m; i++) c[i] += c[i-1]; for(i = n-1; i >= 0; i--) sa[--c[x[i]]] = i; for(int k = 1; k <= n; k <<= 1) { int p = 0; for(i = n-k; i < n; i++) y[p++] = i; for(i = 0; i < n; i++) if(sa[i] >= k) y[p++] = sa[i] - k; for(i = 0; i < m; i++) c[i] = 0; for(i = 0; i < n; i++) c[x[y[i]]]++; for(i = 0; i< m; i++) c[i] += c[i-1]; for(i = n-1; i >= 0; i--) sa[--c[x[y[i]]]] = y[i]; swap(x, y); p = 1; x[sa[0]] = 0; for(i = 1; i < n; i++) x[sa[i]] = y[sa[i-1]] == y[sa[i]] && y[sa[i-1]+k] == y[sa[i]+k] ? p-1 : p++; if(p >= n) break; m = p; } int k = 0; for(i = 0; i < n; i++) ran[sa[i]] = i; for(i = 0; i < n; i++) { if(k) k--; int j = sa[ran[i]-1]; while(s[i+k] == s[j+k]) k++; height[ran[i]] = k; } } void rmq_init() { for(int i=1; i<n; i++) d[i][0] = height[i]; for(int j=1; (1<<j) <= n; j++) for(int i=1; i+(1<<j)-1 < n; i++) d[i][j] = min(d[i][j-1], d[i+(1<<(j-1))][j-1]); } int rmq(int l, int r) { int k = 0; while((1<<(k+1)) <= r-l+1) k++; return min(d[l][k], d[r-(1<<k)+1][k]); } int qp(int l, int r) { l = ran[l], r = ran[r]; if(l > r) swap(l, r); return rmq(l+1, r); //因为height里是等级i和i-1的最长公共前缀 所以是l+1 不然就越界了 } int T; char str[5]; int main() { rd(T); while(T--) { n = 0; int q; rd(q); rep(i, 0, q) { rs(str); s[n++] = str[0] - 'a' + 1; } s[n++] = 0; get_sa(4); rmq_init(); int maxx = -INF, ans; for(int i=1; i<=n; i++) { for(int j=0; j+i<n; j+=i) { ans = qp(j, j+i); int k = j - (i - ans%i); ans = ans/i + 1; //因为j+i的后缀突出来一段长为i的串 所以+1 if(k>=0 && qp(k, k+i) >= i) ans++; maxx = max(maxx, ans); } } cout<< maxx <<endl; } return 0; }