Help Jimmy
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 13669 | Accepted: 4541 |
Description
"Help Jimmy" 是在下图所示的场景上完成的游戏。
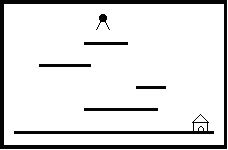
场景中包括多个长度和高度各不相同的平台。地面是最低的平台,高度为零,长度无限。
Jimmy老鼠在时刻0从高于所有平台的某处开始下落,它的下落速度始终为1米/秒。当Jimmy落到某个平台上时,游戏者选择让它向左还是向右跑,它跑动的速度也是1米/秒。当Jimmy跑到平台的边缘时,开始继续下落。Jimmy每次下落的高度不能超过MAX米,不然就会摔死,游戏也会结束。
设计一个程序,计算Jimmy到底地面时可能的最早时间。

场景中包括多个长度和高度各不相同的平台。地面是最低的平台,高度为零,长度无限。
Jimmy老鼠在时刻0从高于所有平台的某处开始下落,它的下落速度始终为1米/秒。当Jimmy落到某个平台上时,游戏者选择让它向左还是向右跑,它跑动的速度也是1米/秒。当Jimmy跑到平台的边缘时,开始继续下落。Jimmy每次下落的高度不能超过MAX米,不然就会摔死,游戏也会结束。
设计一个程序,计算Jimmy到底地面时可能的最早时间。
Input
第一行是测试数据的组数t(0 <= t <= 20)。每组测试数据的第一行是四个整数N,X,Y,MAX,用空格分隔。N是平台的数目(不包括地面),X和Y是Jimmy开始下落的位置的横竖坐标,MAX是一次下落的最大高度。接下来的N行每行描述一个平台,包括三个整数,X1[i],X2[i]和H[i]。H[i]表示平台的高度,X1[i]和X2[i]表示平台左右端点的横坐标。1 <= N <= 1000,-20000 <= X, X1[i], X2[i] <= 20000,0 < H[i] < Y <= 20000(i = 1..N)。所有坐标的单位都是米。
Jimmy的大小和平台的厚度均忽略不计。如果Jimmy恰好落在某个平台的边缘,被视为落在平台上。所有的平台均不重叠或相连。测试数据保证问题一定有解。
Jimmy的大小和平台的厚度均忽略不计。如果Jimmy恰好落在某个平台的边缘,被视为落在平台上。所有的平台均不重叠或相连。测试数据保证问题一定有解。
Output
对输入的每组测试数据,输出一个整数,Jimmy到底地面时可能的最早时间。
Sample Input
1 3 8 17 20 0 10 8 0 10 13 4 14 3
Sample Output23
解析: 用结构体数组存储平台的参数 把起点和地面 也看作平台 然后按照高度排序
题目有两种状态 1、向左走 2、向右走 所以 创建left和right两个函数 (因为需要互相调用 所以要加函数声明) 因为两个函数实现原理相同 所以我们只讨论
一个即可,我们来看left
参数 ans 是当前在的平台 循环是为了找到当前平台下面 挡住老鼠落下的第一个平台 如果没有而且到地面距离又太高 会摔shi的 那么dp【ans】【0】 = INF 即把这个
平台左边到地面所需时间赋为最大值 代表不能通过该左边到达地面
#include <iostream> #include <cstring> #include <cstdio> #include <algorithm> using namespace std; const int maxn = 100010, INF = 9999999; int T,n,x,y,maxx,dp[maxn][2]; int left(int); int right(int); struct node{ int x1,x2,h; }Node[maxn]; int cmp(node a,node b) { return a.h > b.h; } int left(int ans) { if(dp[ans][0]) return dp[ans][0]; if(ans >= n+1) return 0; for(int j=ans+1; j<=n+1; ++j) { if(Node[j].x1 <= Node[ans].x1 && Node[j].x2 >= Node[ans].x1 && Node[ans].h - Node[j].h <= maxx) { left(j); right(j); if(j != n+1) dp[ans][0] = Node[ans].h - Node[j].h + min(dp[j][0] + Node[ans].x1 - Node[j].x1, dp[j][1] + Node[j].x2 - Node[ans].x1); else dp[ans][0] = Node[ans].h; break; } else dp[ans][0] = INF; } } int right(int ans) { if(dp[ans][1]) return dp[ans][1]; if(ans >= n+1) return 0; for(int j=ans+1; j<=n+1; ++j) { if(Node[j].x1 <= Node[ans].x2 && Node[j].x2 >= Node[ans].x2 && Node[ans].h - Node[j].h <= maxx) { left(j); right(j); if(j != n+1) dp[ans][1] = Node[ans].h - Node[j].h + min(dp[j][1] + Node[j].x2 - Node[ans].x2, dp[j][0] + Node[ans].x2 - Node[j].x1); else dp[ans][1] = Node[ans].h; break; } else dp[ans][1] = INF; } } int main() { cin>>T; while(T--) { memset(dp,0,sizeof(dp)); memset(Node,0,sizeof(Node)); cin>>n>>x>>y>>maxx; Node[0].x1 = Node[0].x2 = x; Node[0].h = y; //把起点放进数组 for(int i=1;i<=n;i++) { cin>>Node[i].x1>>Node[i].x2>>Node[i].h; } Node[n+1].x1 = -20001; Node[n+1].x2 = 20001; Node[n+1].h = 0; //把地面放进数组 sort(Node,Node+n+2,cmp); // for(int i=0;i<=n+1;i++) // cout<<Node[i].x1<<" "<<Node[i].x2<<" "<<Node[i].h<<endl; // left(0); right(0); cout<<min(dp[0][1], dp[0][0])<<endl; } return 0; }