剑指 Offer II 029. 排序的循环链表

给定循环单调非递减列表中的一个点，写一个函数向这个列表中插入一个新元素 insertVal ，使这个列表仍然是循环升序的。

给定的可以是这个列表中任意一个顶点的指针，并不一定是这个列表中最小元素的指针。

如果有多个满足条件的插入位置，可以选择任意一个位置插入新的值，插入后整个列表仍然保持有序。

如果列表为空（给定的节点是 null），需要创建一个循环有序列表并返回这个节点。否则。请返回原先给定的节点。

 

示例 1：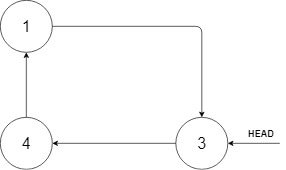

 

输入：head = [3,4,1], insertVal = 2
输出：[3,4,1,2]
解释：在上图中，有一个包含三个元素的循环有序列表，你获得值为 3 的节点的指针，我们需要向表中插入元素 2 。新插入的节点应该在 1 和 3 之间，插入之后，整个列表如上图所示，最后返回节点 3 。


示例 2：

输入：head = [], insertVal = 1
输出：[1]
解释：列表为空（给定的节点是 null），创建一个循环有序列表并返回这个节点。

示例 3：

输入：head = [1], insertVal = 0
输出：[1,0]

 

提示：

    0 <= Number of Nodes <= 5 * 10^4
    -10^6 <= Node.val <= 10^6
    -10^6 <= insertVal <= 10^6

解析：

　　放到vector里，找到最小的第一个元素的位置id，排序，lower_bound找到第一个大于等于insertVal的位置x

k = id + x，就是从head走多少步到插入这个数的位置，k - 1就是前驱节点的位置

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* next;

    Node() {}

    Node(int _val) {
        val = _val;
        next = NULL;
    }

    Node(int _val, Node* _next) {
        val = _val;
        next = _next;
    }
};
*/

class Solution {
public:
    Node* insert(Node* head, int insertVal) {
        // not write null
        if(head == nullptr)
        {
            Node* temp = new Node(insertVal);
            temp->next = temp;
            head = temp;
            return head;
        }


        vector<int> nums;
        Node* p = head;
        nums.push_back(p->val);
        p = p->next;
        while(p != head)
        {
            nums.push_back(p->val);
            p = p->next;
        }
        int minx = nums[0], id = 0;
        for(int i = 0; i < nums.size(); i++)
        {
            if(minx > nums[i])
            {
                minx = nums[i];
                id = i;
            }
        }
        if(id == 0)
        {
            int j = nums.size() - 1;
            while(j >= 0 && nums[j] == minx)
                j--;
            j++;
            if(j < nums.size())
                id = j;
        }
        sort(nums.begin(), nums.end());
        int x = lower_bound(nums.begin(), nums.end(), insertVal) - nums.begin();
        int k = id + x - 1;
        p = head;
        k = (k == -1 ? k + nums.size() : k);
        while(k > 0)
        {
            k--;
            p = p->next;
        }
        Node* temp = new Node(insertVal, p->next);
        p->next = temp;

        return head;
        
    }
};