一年前写的了。。。今天又翻出来了
这是一年前我做的数论题的部分总结。。。。。
（1）一个大于1的正整数N，如果它的标准分解式为：
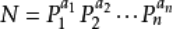
，那么它的正因数个数为
对于这个式子 如果我们想要奇因子的个数 那么在primes[i] % 2 != 0时再算。。==0时continue就好了 偶因子同理
（2） 它的全体正因数之和为
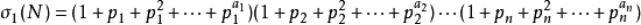
1、算术基本定理求质因子、正因子的个数（奇因子的个数，偶因子的个数，1）、全体正因数之和
2、10^18 和 2^64的范围出现时用ULL
3、有两个未知量时，可以遍历一个求另一个
https://www.cnblogs.com/WTSRUVF/p/9341686.html
4、需要画图时一定要画图，不能想当然
https://www.cnblogs.com/WTSRUVF/p/9334837.html
5、循环边界为n时 观察是否能降低为sqrt（n）；
6、N/i 小于N的且是i的倍数的个数(小于N且能被i整除的数的个数)
7、求数N的后缀零 N = 10^k*m = 2^k1 * 5^k2 * m,即求k的最大值，即求max（k1， k2）；
预处理每个 1 - 1e6 的每个数字的对2分解，对5分解的次数
8、求两点间 （x1，y1） 和 （x2， y2）线段上的整点的个数；（x1，y1，x2，y2均为整数）求gcd(abs(x1-x2), abs(y1-y2));
若x1，y1，x2，y2均为0.1的整数倍 则用欧几里得求解
根据两点式公式求出直线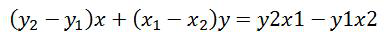
，那么ax+by=c 中的a、b、c都可以确定下来了。
接下来首先去计算出一组解(x0,y0)，因为根据这一组解，你可以写出它的任意解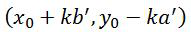
，其中
，K取任何整数。
需要注意的是，这个 a' 和 b' 是很重要的，比如说 b' ，它代表的是x每隔 b' ，就会出现一个整点。
所以这道题目的关键就是，我们先求出一组解，然后通过它的 b' 将x0改变成x，使得x在[x1,x2]区间之内，这样每 b' 个单位就有一个整点了，即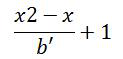
题目：https://www.cnblogs.com/WTSRUVF/p/9325081.html
9、求 n 的阶乘在 base 进制下的位数，这里有一个简单的方法，就是log10（n）+ 1就是 n 的在十进制下的位数（想一下 为什么。。。），由此可知 log base（n）+ 1 就是n在base 进制下的位数，再根据换底公式，log base（n） == log（n）/ log（base），这里让求的是阶乘，根据log的原理呢，就有log base （n！） == （ log（n） + log（n-1） + log（n-2） + 。。。。+ log（1）） / log（base）。用 sum 数组存一下 log（n！) 就可以快速的求出了
10、整数N有多少个别的进制的数有后导零 = N的因子的个
https://www.cnblogs.com/WTSRUVF/p/9342230.html
11、威尔逊定理如果p为素数则
( p -1 )! ≡ -1 ( mod p ) 即 （p-1）！+1 为 p的整数倍
11、等差数列前n项和公式Sn=n(a1+an)/2
Sn=na1+n(n-1)d/2
12、梅林素数：满足 E = 2 ^ i - 1 的数称为梅林数 E如果是素数则为梅森素数 “一个数能够写成几个不重复的梅森素数的乘积” 等价于 “这个数的约数和是2的幂次”
并且这个2的幂（指数）正好等于作为因子的梅森素数的梅森指数的和。
例： 3 (2的2次幂-1) X 7 (2的3次幂-1) = 21;
21的因数和1+3+7+21=32=2^5; 这个 2的幂 5 = 2 + 3；
int 范围内的梅林素数
//梅林素数
int mason[8]={3,7,31,127,8191,131071,524287,2147483647};
//梅林素数对应的梅林指数
int ans[8]={2,3,5,7,13,17,19,31};
13、大区间求素数：
求出来[0,sqrt(b)]的素数 然后取倍数删去[a,b]之间的合数
int main()
{
init();
int T;
int kase = 0;
LL a, b;
cin>> T;
while(T--)
{
int res = 0;
mem(bz,0);
cin>> a >> b;
// if(a <= 2) a = 2;
int len = b - a;
for(int i=0; i<ans && primes[i] * primes[i] < b; i++)
{
int j = a/primes[i];
if(j*primes[i] < a) j++; // 我们要找到第一个大于等于a的合数，因为出的时候是向下取整 所以要判断一下
if(j <= 1) j++; // 如果j == 1 则说明 a是一个质数 但我们要找合数
{
bz[j*primes[i] - a] = 1;
j++;
}
}
if(a == 1) bz[0] = 1; // a == 1时要特殊讨论 因为1不是一个合数，无法由比它小的质数组成，也不是一个质数，所以在标记bz数组时 没有标记 就会多算
for(int k=0; k<=len; k++)
if(!bz[k])
res++;
printf("Case %d: %d ",++kase,res);
}
return 0;
}
14、BigInteger 二分开方：
public static BigInteger sqrt( BigInteger n ) {
BigInteger L = BigInteger.ZERO , R = n ;
while ( L.compareTo(R) < 0 ) {
BigInteger M = L.add(R) ;
M = M.divide(BigInteger.valueOf(2)) ;
if ( M.multiply(M).compareTo(n) == 0 ) return M ;
else if ( M.multiply(M).compareTo(n) > 0 ) R = M.subtract(BigInteger.ONE);
else if(M.multiply(M).compareTo(n) < 0) L = M.add(BigInteger.ONE) ;
}
return L ;
}
15、多项式域欧几里得模板：
求多项式的最大公约数
例：给定两个Zn上的多项式f和g，求出它们的gcd，并且次数尽量大，最高项系数为1（加法和乘法均在mod m意义下进行）
#include <stdio.h>
#include <string.h>
#include <vector>using namespace std;int n;
vector<int> f, g;
// 快速幂求逆元int inv(int a, int n) {
int res = 1;
int b = n-2;
while(b)
{
if(b & 1) res = res * a % n;
a = a * a % n;
b >>= 1;
}
return res;
}
//多项式的最大公约数
vector<int> gcd(vector<int> a,vector<int> b)
{
if(b.size() == 0) return a;
int t = a.size() - b.size();
vector<int> c;
for(int i=0; i<=t; i++)
{
int tmp = a[i] * inv(b[0],n) % n;
for(int j=0; j<b.size(); j++)
a[i+j] = (a[i+j] - tmp * b[j] % n + n) % n;
}
int p = -1;
for(int i=0; i<a.size(); i++)
{
if(a[i] != 0)
{
p=i;
break;
}
}
if(p >= 0)
for(int i=p; i<a.size(); i++)
c.push_back(a[i]);
return gcd(b,c);
}
int main() {
int cas = 0;
while (~scanf("%d", &n) && n) {
f.clear(); g.clear();
int a, k;
scanf("%d", &a);
for (int i = 0; i <= a; i++)
{
scanf("%d", &k);
f.push_back(k);
}
scanf("%d", &a);
for (int i = 0; i <= a; i++)
{
scanf("%d", &k);
g.push_back(k);
}
vector<int> ans = gcd(f, g);
int tmp = inv(ans[0], n), ansz = ans.size();
printf("Case %d: %d", ++cas, ansz - 1);
for (int i = 0; i < ansz; i++)
{
printf(" %d", ans[i] * tmp % n);
}
printf(" ");
}
return 0;
}
16、指数循环节：
LL dfs(LL cnt, LL m)
{
if(cnt == n-1)
{
return num[cnt] % m;
}
LL phi = A[m];
LL k = dfs(cnt+1, phi) + phi; //因为在上一步的快速幂中已经%phi 所有这一步不用%phi
return qpow(num[cnt], k, m);
}
17、
暴力的时候想一下是否某一步可以预处理简化一下步骤
例：UVA-11728
18、gcd与phi
设gcd（x，i） = m 即x和i的最大公约数为m 则x/m 和 i/m 互质 然后我们求出于i/m互质的有多少个 是不是就是求出了与i最大公约数为m的有多少个。。用欧拉函数既能求出个数 。。。即为phi（i/m）个
https://www.cnblogs.com/WTSRUVF/p/9306386.html
19、
一个数N一共包含了几个5，那么N!就会有几个零；比如，
5以及5之前的数一共包含了1个5，所以末尾共有1个零；
20以及20之前的数一共包含了4个5（5自身为1个,10包含一个，15包含一个，20包含一个），所以末尾共有4个零；
25以及25之前的数一共包含了6个5（5,10各包含一个，15包含一个，20包含一个，25包含两个（5*5等于25，所以25包含两个）），所以末尾共有6个零；
28以及28之前的数一共包含了6个5，所以末尾共有6个零；
LL count(LL x)
{
int cnt = 0;
while(x)
{
cnt += x / 5;
x /= 5;
}
return cnt;
}
20、
给出一个数x 求 x = bp 的p的最大值
解析：
算术基本定理 分解质因数
任何一个数x都可以表示为 x == p1a1 * p2a2 * ````` * pnan
即 bp == p1a1 * p2a2 * ````` * pnan == (p1b1 * p2b2 * `````` * pnbn)p
所以 pmax == gcd（a1，a2，·····，an）；
如果x是一个负数 则p只能为奇数
先把x换成正数求出最大p之后 如果x 为负 则不断除2 直至p为奇数
21、
分段打表
例：求调和级数 (1 <= n <= 10^8)
每间隔50存储一个数，在计算时 只需要找到离输入的n最近的那个数 以它为起点 开始计算即可
double ch[maxn/50+10];int main()
{
int T, cnt = 1;
double sum = 0;
ch[0] = 0;
for(int i=1; i<=maxn; i++)
{
sum += 1/(double)i;
if(i % 50 == 0)
ch[cnt++] = sum;
}
int kase = 0;
cin>> T;
while(T--)
{
int n;
cin>> n;
double m = ch[n/50];
for(int i=n/50*50+1; i<=n; i++)
m += 1/(double)i;
printf("Case %d: %.10f ",++kase,m);
}
22、
1-n中有多少对a 和 b 的最小公倍数为n （a <= b）
有序对(a,b)方案数就是(2k1+1)(2k2+1)⋯(2ks+1)，
无序对(a,b)方案数就是:{[(2k1+1)(2k2+1)⋯(2ks+1)] + 1}/2
k为n的每个质因子的幂
23、
哥德巴赫猜想：任意一个偶数 都可以分解成两个（就是一对啦）质数的加和
证明哥德巴赫猜想：
素数打表。。因为 质数 + 质数 = 偶数 所以 偶数 - 质数 = 质数
23、
任何一个数N == 10^a a可以为小数
设a == x+y （x为整数部分，y为小数部分），则10^x用来决定位数 10^y是这个数字的有效部分
此条结论可以用来求n的k次方的前三位
任何一个数n均可以表示为10a， 其中 a 可以为小数
那么nk 可以表示为10ak ， 令ak == x + y （其中x为整数 y为小数） 所以 ak - x == y
于x是整数，那么很明显他是用来指定位数的，因为10x肯定是一个10， 100， 10000...之类的数字，也就是说10y才是这个数字的有效部分，我们只要求出10y，然后乘上100最终结果就是我们想要的。
因为n = 10a 所以 a = log10(n)，10y就是小数部分，我们用函数fmod(ak, 1)，返回ak 的小数部分，然后乘上100即可
fmod返回的是y的值，所以必须计算10y才是真实值，所以直接使用102 * 10y 即pow(10, 2 + y)；
24、
平方数 及其 平方数的2倍 的约数和为奇数
25、
完全平方数分解质因子后每个质因子的指数都为偶数
26、
一看到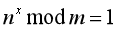
（
）
就一定要想到如果n和m互质那么n^Φ(m) mod m = 1
且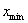
| Φ(m)