一个问题的产生
与笔者同一年代的人应该都有这样的共同记忆:一个炎日的夏日,坐在沙发上,吃着冰爽的西瓜,看DVD中的迪迦奥特曼动画片,这样悠闲的时光即使是短暂的回忆起也令人神往。But nothing can always be perfect,最令人痛心的莫过于碟片光洁的背面产生了划痕,一道巨大的划痕常常意味着我们变不成光。但好在这样的事情不会经常发生,甚至不可思议的一些较浅的划痕并不会影响动画片的正常播放。

这件看似平常的事情现在回想起似乎是不合逻辑的。DVD光盘上无数的小坑储存着0和1,划痕导致了光盘上数据的损失,且这些损失数据所在的位置是随机的。那么如果直接读取这些信息,光盘上储存的视频信息必然无法正常播放。

由此我们不难推断出,一定有某种纠错的机制修复了(至少在某种程度上)这些缺损的信息。那这样的修复机制是如何实现的呢?
一个很直接的思路就是进行备份。方法也很简单,我们如果能将这一份数据备份三份,那么我们只需要检测某一位置上数字与其他两份是否相同,就能在很大程度上修复错误的信息。然而如此大的冗余量明显是不切合实际的。那么有没有一种方法既能检验并修复出传输过程的错误(噪音),又只产生尽可能小的冗余呢?
奇偶效验(Parity Check)
相信聪明的你不难发现,检验错误和读取信息之间有着本质上的不同。前者只需检验信息流的某一特征来回答是或否的问题,而后者则需要读取信息流全部的信息。那么对于一个仅由0、1组成的信息串,最显著的特征无疑是0或1的总数。那么将0或1的个数作为冗余来检验错误是否可行呢?可行,但难以操作。因为对于一个未知的信息流,我们难以确定所需要的冗余位数。
好在数字的奇偶特性为我们提供一种更为实际的检验方法。对于任意长度的数据,仅需一位额外的空间开销便可确定其奇偶性特征,因此满足我们对于冗余尽可能小的要求。并且由于单个位上仅存在0、1两种状态,那么如果我们知道了发生错误的位,若将该位取反,还可以恢复数据(消除噪音)。这种方法便是大名鼎鼎的奇偶效验。
奇偶校验是一种添加一个奇偶位用来指示之前的数据中包含有奇数还是偶数个1的检验方式。如果在传输的过程中,有奇数个位发生了改变,那么这个错误将被检测出来(注意奇偶位本身也可能改变)。一般来说,如果数据中包含有奇数个1的话,则将奇偶位设定为1;反之,如果数据中有偶数个1的话,则将奇偶位设定为0。换句话说,原始数据和奇偶位组成的新数据中,将总共包含偶数个1.
读到这里,你一定会提出疑问:如果同时有两个位上的1发生了改变,这样的情况如何处理呢?是的,奇偶校验并非总是有效,如果数据中有偶数个位发生变化,则奇偶位仍将是正确的,因此不能检测出错误。而且,即使奇偶校验检测出了错误,它也不能指出哪一位出现了错误,从而难以进行更正。数据必须整体丢弃并且重新传输。在一个“容易出错”(噪音较大)的媒介中,成功传输数据可能需要很长时间甚至不可能完成。
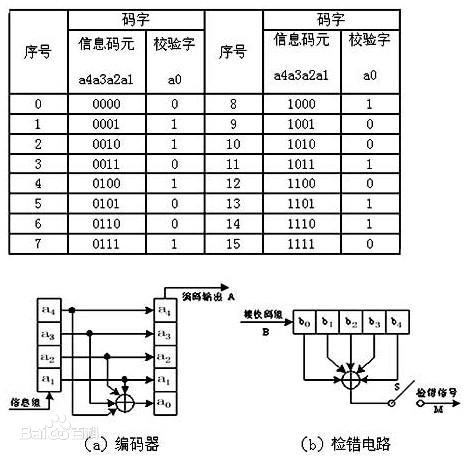
做到这一步的我们不想放弃,那能否在奇偶检验的方法上做出改进,使其能发现出现错误的位置以加以修复呢?1940年代晚期,在贝尔实验室(Bell Labs)工作的理查德·卫斯里·汉明(Richard Wesley Hamming)因读卡机不可靠而频繁发生错误而十分沮丧。他遇到了和我们现在相似的困扰,因此开始逐步开发功能日益强大的侦错算法。在1950年,他发表了一种线性纠错码,巧妙地解决了这一问题,这便是我们现在所熟知的汉明码(Hamming code)。

汉明码(Hamming code)
记得在一次部门聚会上,一个学长提出玩这样一个小游戏。游戏的规则很简单,主持人先会讲述一个离奇的事实,而游玩者通过不断向主持人提出是或否的问题,最后推断出故事的真相。汉明码正是采用了这样的思路以确定了错误产生的位置。
算法如下
从1开始给数字的数据位(从左向右)标上序号, 1,2,3,4,5...
将这些数据位的位置序号转换为二进制,1, 10, 11, 100, 101,等。
数据位的位置序号中所有为二的幂次方的位(编号1,2,4,8,等,即数据位位置序号的二进制表示中只有一个1)是校验位
所有其它位置的数据位(数据位位置序号的二进制表示中至少2个是1)是数据位
每一位的数据包含在特定的两个或两个以上的校验位中,这些校验位取决于这些数据位的位置数值的二进制表示
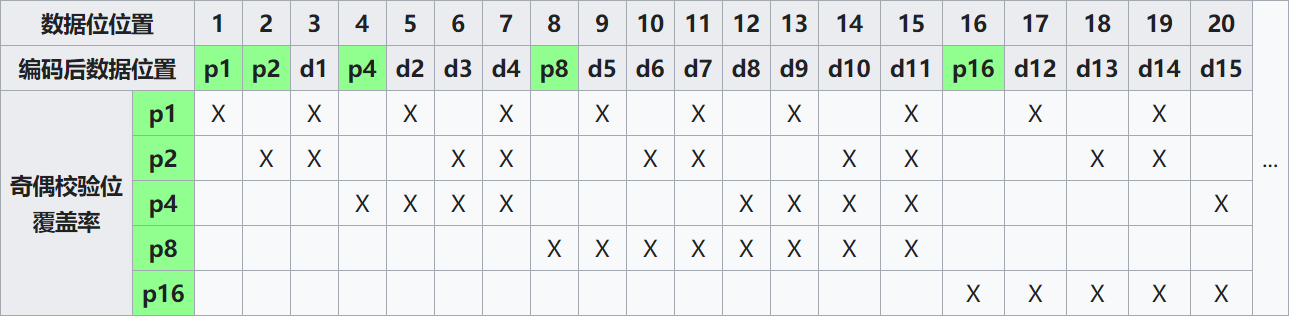
①校验位1覆盖了所有数据位位置序号的二进制表示倒数第一位是1的数据:1(校验位自身,这里都是二进制,下同),11,101,111,1001,等
②校验位2覆盖了所有数据位位置序号的二进制表示倒数第二位是1的数据:10(校验位自身),11,110,111,1010,1011,等
③校验位4覆盖了所有数据位位置序号的二进制表示倒数第三位是1的数据:100(校验位自身),101,110,111,1100,1101,1110,1111,等
④校验位8覆盖了所有数据位位置序号的二进制表示倒数第四位是1的数据:1000(校验位自身),1001,1010,1011,1100,1101,1110,1111,等
⑤简而言之,所有校验位覆盖了数据位置和该校验位位置的二进制与的值不为0的数。
通过对校验位进行检测,我们便可逐步锁定错误发生的位置。值得一提的是无论采用奇校验还是偶校验都是可行的。偶校验从数学的角度看更简单一些,但在实践中并没有区别。
理解汉明码算法
上述的算法描述有些抽象,为了便于理解汉明码算法,我们不妨做一个简单的游戏。
在这个游戏中包含发送者(sender)和接受者(receiver)两个玩家。发送者会发送一个16bit的数据块,其中包含了11bit的有效信息。然而在传输过程中,某一位可能发生变化。接受者需要根据4位冗余的信息,确定发生错误的位置。
为了直观地表现数据的形式,我们不妨将16bit的数据块表示为4*4的矩阵形式,并将其根据从左到右、从上到下的顺序编号为0~15。其中2的n次方位为检验为,n为自然数。

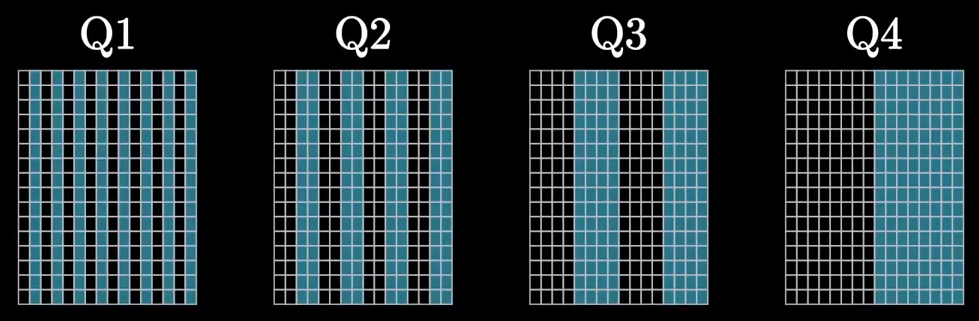
因此,编号为1的空格为第一个检验位,负责检验2,4列的奇偶检验,即保证2,4列中1的个数一定为偶数。

编号为2的空格为第二个检验位,负责检验3,4列的奇偶检验。

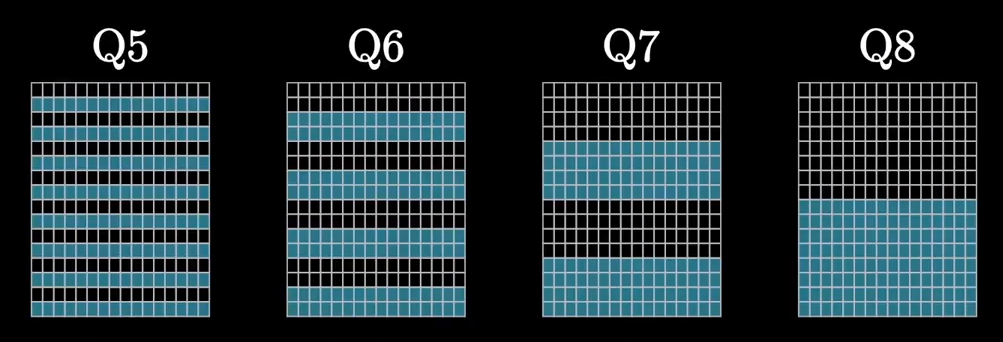
编号为4的空格为第三个检验位,负责2,4行的奇偶检验。
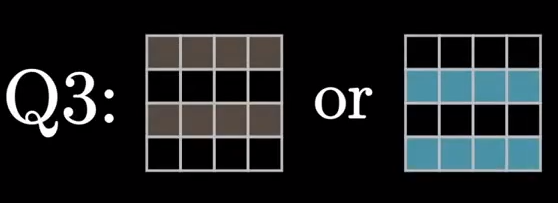
编号为8的空格为最后一个检验位,负责3,4行的奇偶检验。
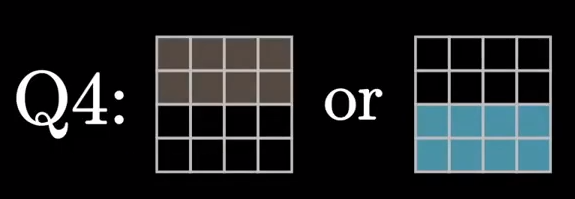
由此我们仅需依次对四个校验位进行效验,即可最终确定错误发生的位置。
到这里你一定会提出这样的疑问,0位是否多余呢?事实上0位确实可以忽略,但我们可以将0位作为整体的奇偶检验位,这样便能检验出是否发生了两个位的变化(尽管我们并不能知道这两个位的具体位置)。
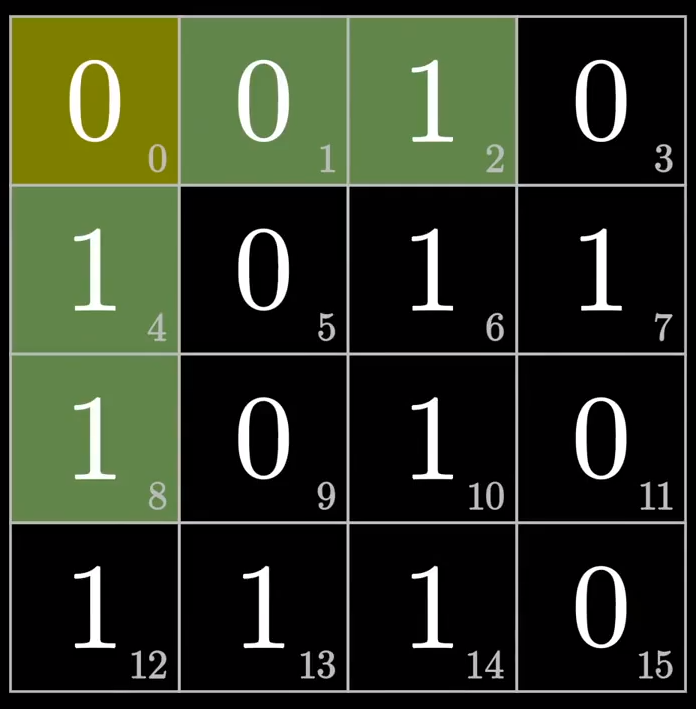
比如发送者发出的数据为00110001110(11位),如图
聪明的你不妨花一点时间,根据刚才的方法填写下检验位的数据。
现在公布答案,分别为0、0、1、1、1。
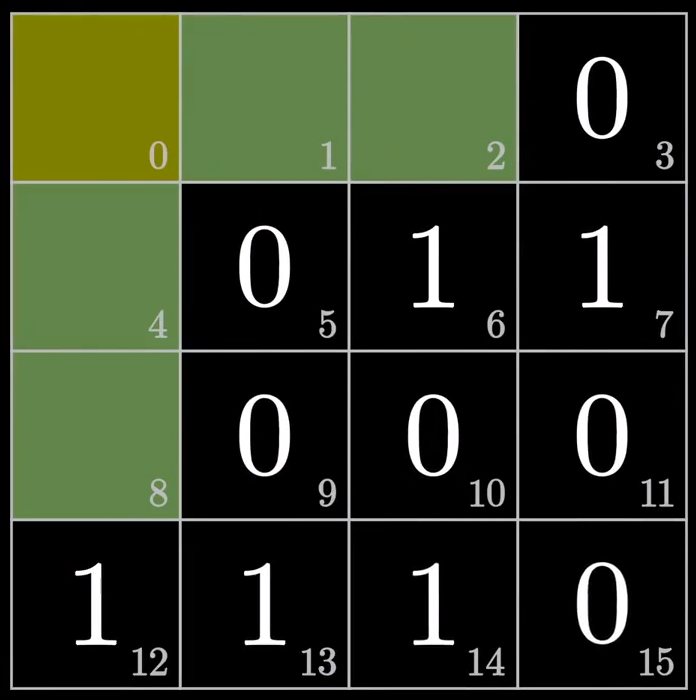
假设经过传输后,接受者收到的数据块如下图所示,这里其实发生了数据错误,根据刚才的检验方法,你找出发生错误的位置了吗?
可以看到校验位2与校验位8对应的校验范围内1的个数为奇数,不符合我们的编码规则,所以是第8+2=10位(1010)的数字反了,即10位上的1应该是0。
有兴趣的话,你还可以选择其它的数据,进行该游戏。
对于更长的数据块我们同样能依据上述的规律进行的检验。随着数据量的增大,你会发现汉明码算法的简洁与优雅是如此的惊人。
对下一期的预告
本期我们对汉明码的算法原理有了一定的了解,下一期我们将进一步阐述该算法的代码实现,由此你能深入领略该算法的精妙之处,