SPFA算法

定义

SPFA 算法是 Bellman-Ford算法 的队列优化算法的别称，通常用于求含负权边的单源最短路径，以及判负权环。

原理

动态逼近法：

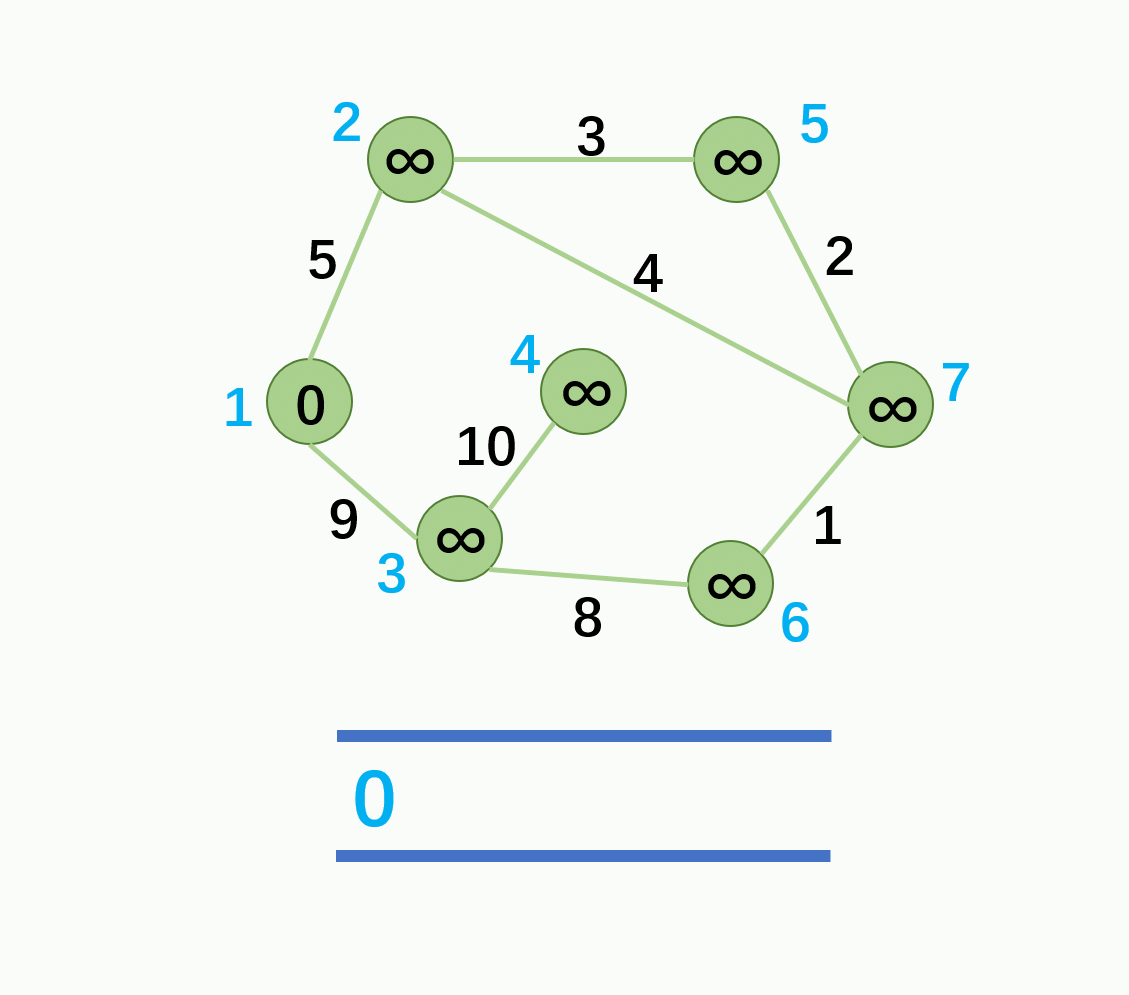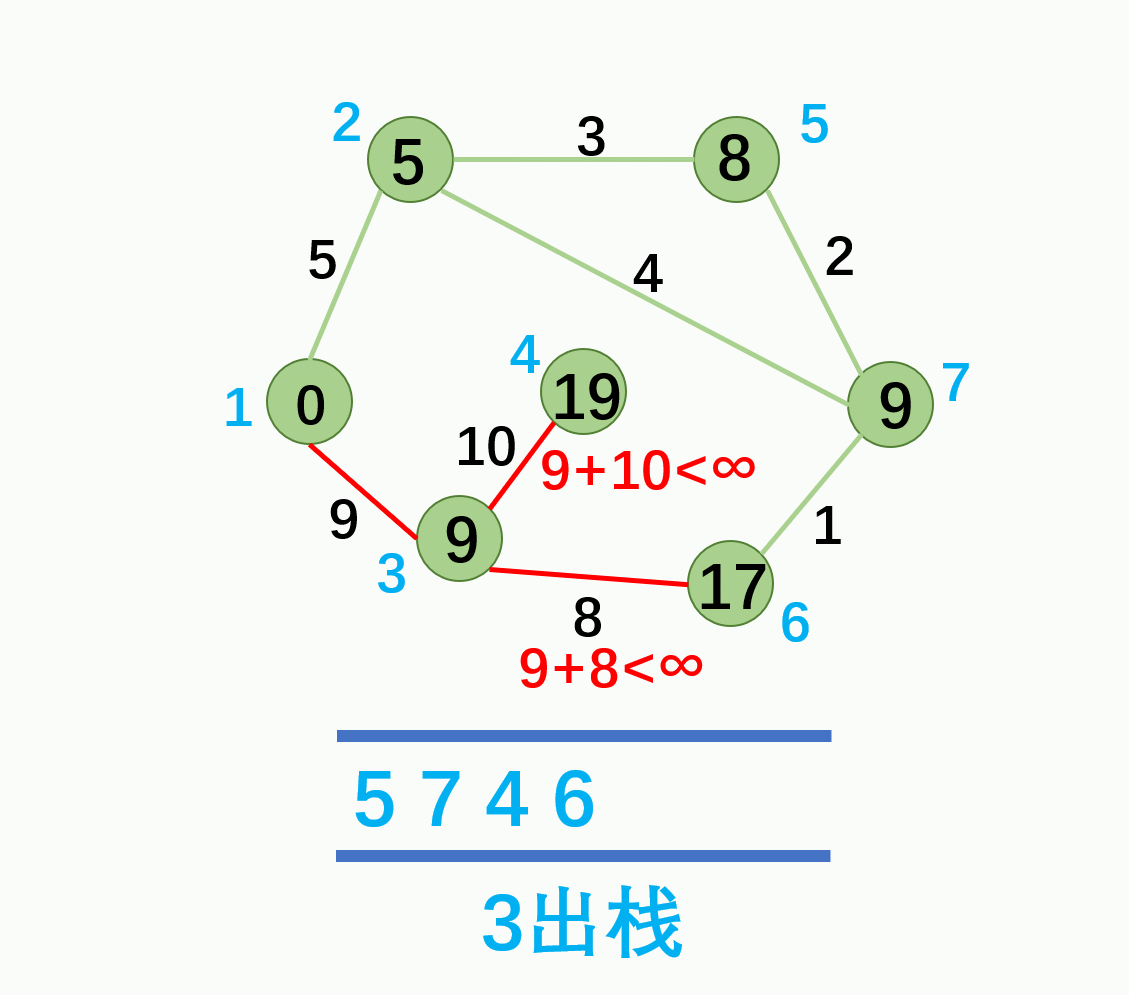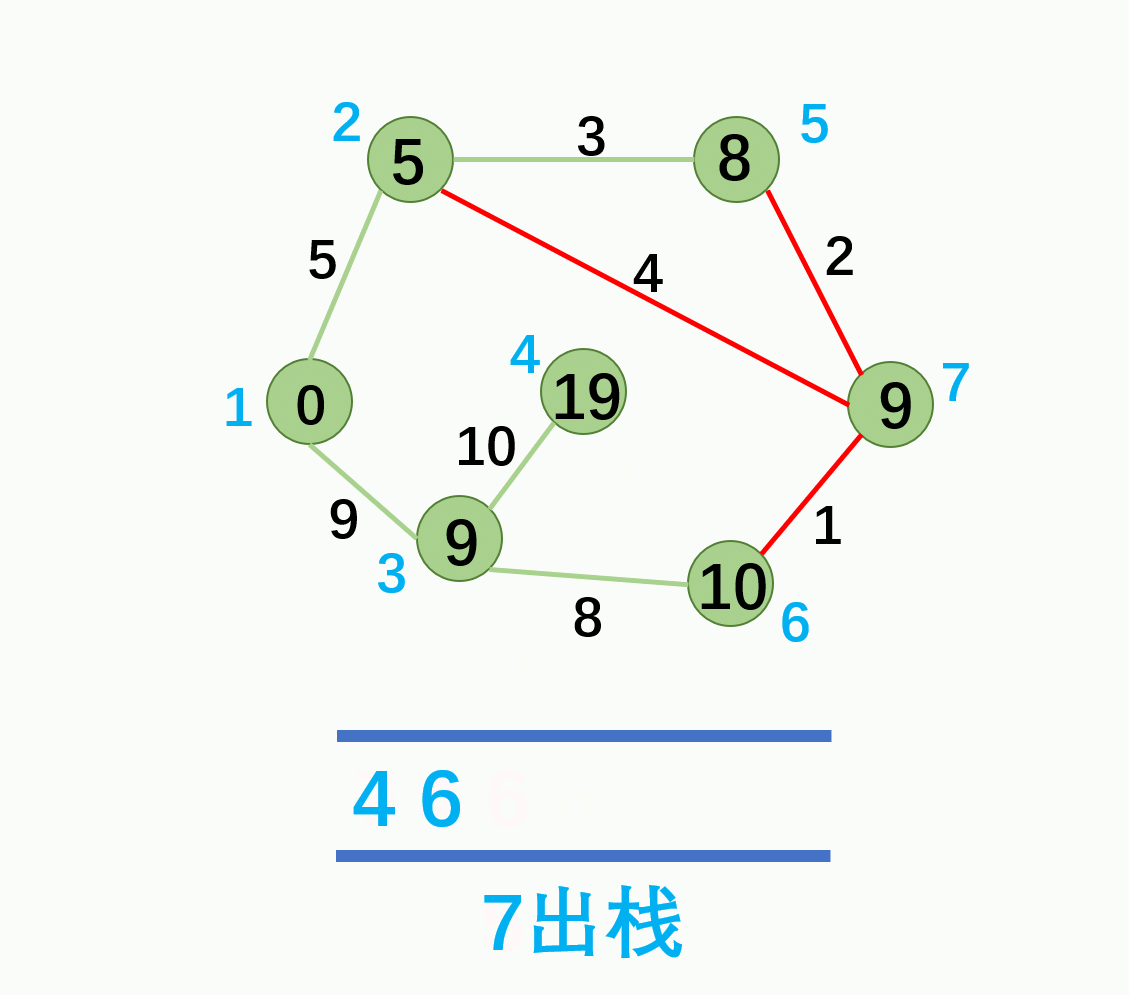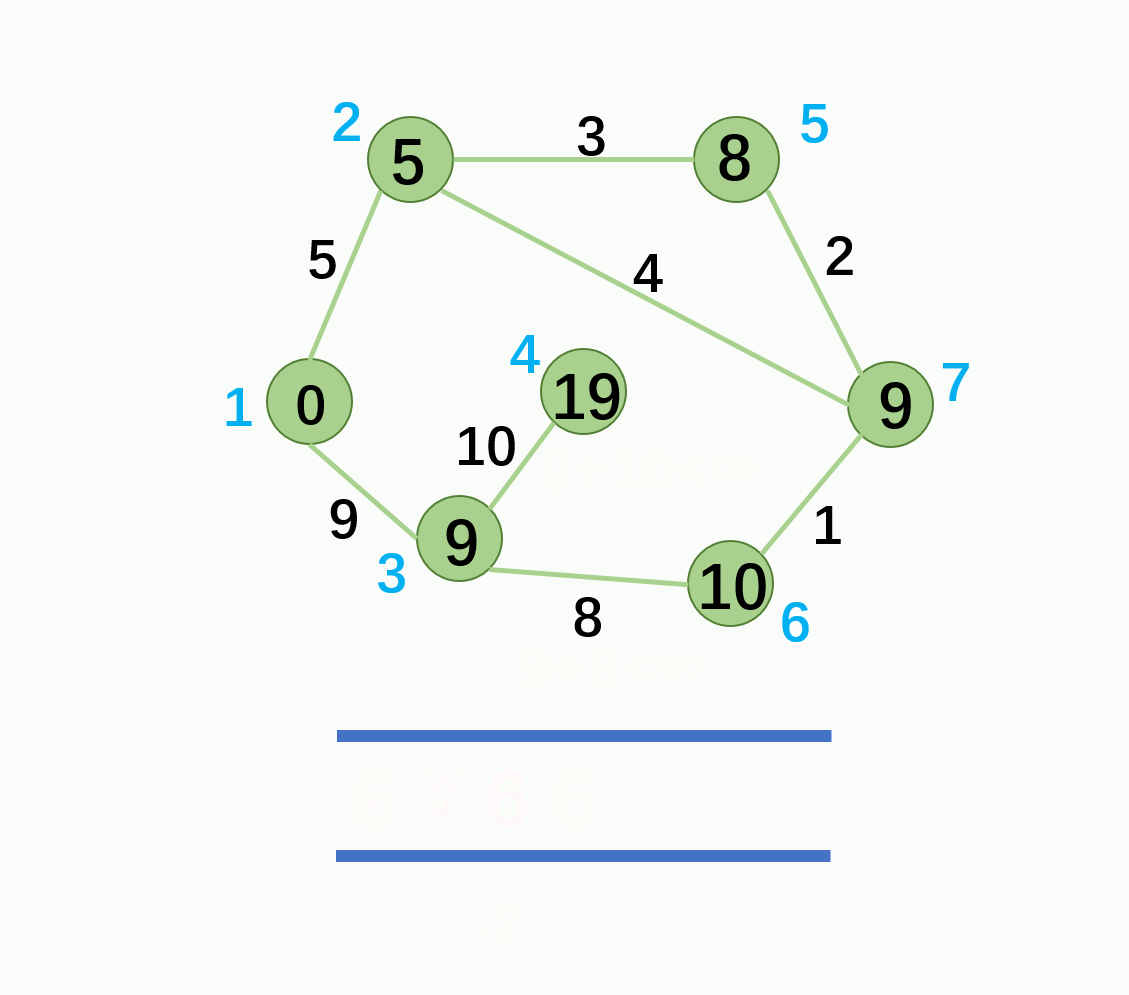
①  设立一个队列用来保存待优化的结点。

②  优化时每次取出队首结点 u，并且用 u 点当前的最短路径估计值对 u 点所指向的结点 v 进行松弛操作，如果 v 点的最短路径估计值有所调整，且 v 点不在当前的队列中，就将 v 点放入队尾。

③  这样不断从队列中取出结点来进行松弛操作，直至队列空为止。

    如果某个点进入队列的次数超过 N 次则存在负环。

 松弛操作利用三角不等式：“三角形两边之和大于第三边”。

 所谓对结点 i, j 进行松弛，就是判定是否 dis[j] > dis[i] + w[i,j]，如果该式成立，则 dis[j] = dis[i] + w[i,j]，反之不变。

 简单地说，如果一个点的最短路被更新了，那么需要判断与此点连接的其他点是否也需要更新。

实现

代码

#include<bits/stdc++.h>
using namespace std;
const int maxn=1005;
const int inf=0x3f3f3f3f;
struct node
{
  int v,w;
  node(){}
  node(int a,int b) {v=a;w=b;}
};
int n,m;
vector<node> e[maxn];
void SPFA(int s);
int main()
{
  int i,u,v,w;
  scanf("%d%d",&n,&m);
  for(i=1;i<=m;i++)
  {
    scanf("%d%d%d",&u,&v,&w);
    e[u].push_back(node(v,w));
  }
  SPFA(1);
  system("pause");
  return 0;
}
void SPFA(int s)
{
  int i,p,v,w,dis[maxn],vis[maxn]={0},cnt[maxn]={0};
  queue<int> que;
  fill(dis,dis+maxn,inf);
  que.push(s);
  dis[s]=0;
  while(!que.empty())
  {
    p=que.front();que.pop();
    vis[p]=0;cnt[p]++;
    if(cnt[p]==n+1) //有环
      {printf("有环
");return ;}
    for(i=0;i<e[p].size();i++)
    {
      v=e[p][i].v;
      w=e[p][i].w;
      if(dis[v]>dis[p]+w)
      {
        dis[v]=dis[p]+w;
        if(!vis[v])
        {
          vis[v]=1;
          que.push(v);
        }
      }
    }
  }
  printf("%d
",dis[n]); //1->n 最短路
}

关于SPFA，他死了

SLF（Small Label First）优化

原队列改为双端队列，对一个要加入队列的点 u，如果dis[u] 小于队首元素 v 的dis[v]，那么就加入到队首元素，否则加入到队尾。

#include<bits/stdc++.h>
using namespace std;
const int maxn=1005;
const int inf=0x3f3f3f3f;
struct node
{
  int v,w;
  node(){}
  node(int a,int b) {v=a;w=b;}
};
int n,m;
vector<node> e[maxn];
void SPFA(int s);
int main()
{
  int i,u,v,w;
  scanf("%d%d",&n,&m);
  for(i=1;i<=m;i++)
  {
    scanf("%d%d%d",&u,&v,&w);
    e[u].push_back(node(v,w));
  }
  SPFA(1);
  system("pause");
  return 0;
}
void SPFA(int s)
{
  int i,p,v,w,dis[maxn],vis[maxn]={0};
  deque<int> Q;
  fill(dis,dis+maxn,inf);
  Q.push_back(s);
  dis[s]=0;
  while(!Q.empty()) 
  {
    p=Q.front();Q.pop_front();
    vis[p]=0;
    for(i=0;i<e[p].size();i++) 
    {
      v=e[p][i].v;
      w=e[p][i].w;
      if(dis[v]>dis[p]+w) 
      {
        dis[v]=dis[p]+w;
        if(!vis[v]) 
        {
          vis[v]=1;
          if(!Q.empty()&&dis[v]<dis[Q.front()]) Q.push_front(v);
          else Q.push_back(v);
        }
      }
    }
  }
  printf("%d
",dis[n]); //1->n 最短路
}

LLL（Large Label Last）优化

令队首元素为 k ，每次松弛时进行判断，队列中所有 dis 值的平均值为 x 。

若 dis[k] > x ，则将 k 插入到队尾，查找下一元素，直到找到某一个 k 使得 dis[k] <= x ，则将 k 出队进行松弛操作。

#include<bits/stdc++.h>
using namespace std;
const int maxn=1005;
const int inf=0x3f3f3f3f;
struct node
{
  int v,w;
  node(){}
  node(int a,int b) {v=a;w=b;}
};
int n,m;
vector<node> e[maxn];
void SPFA(int s);
int main()
{
  int i,u,v,w;
  scanf("%d%d",&n,&m);
  for(i=1;i<=m;i++)
  {
    scanf("%d%d%d",&u,&v,&w);
    e[u].push_back(node(v,w));
  }
  SPFA(1);
  system("pause");
  return 0;
}
void SPFA(int s)
{
  int i,p,v,w,dis[maxn],vis[maxn]={0},num=1,sum=0;
  deque<int> Q;
  fill(dis,dis+maxn,inf);
  dis[s]=0;vis[s]=1;
  Q.push_back(s);
  while(!Q.empty())
  {
    p=Q.front();Q.pop_front();
    num--;sum-=dis[p];
    while(dis[p]*num>sum)
    {
      Q.push_back(p);
      p=Q.front();
      Q.pop_front();
    }
    vis[p]=0;
    for(i=0;i<e[p].size();i++) 
    {
      v=e[p][i].v;
      w=e[p][i].w;
      if(dis[v]>dis[p]+w) 
      {
        dis[v]=dis[p]+w;
        if(!vis[v])
        {
          vis[v]=1;
          if(!Q.empty()&&dis[v]<=dis[Q.front()]) Q.push_front(v);
          else Q.push_back(v); 
          num++;sum+=dis[v];
        }
      }
    }
  }
  printf("%d
",dis[n]); //1->n 最短路
}

                                                                                                  优化了也没蛋用，想卡你照样卡你。淦