Description
首先给出一个只包含小写字母和'B'、'P'的操作序列(s_0(|s_0|leq10^5))。初始时我们有一个空串(t),依次按(s_0)的每一位进行操作:
- 如果是小写字母,则在(t)后面加入这个小写字母;
- 如果是'B',则删除(t)的最后一位;
- 如果是'P',则复制t到集合(S)中。
操作结束后,集合中有(n(nleq10^5))个字符串,将它们按加入集合的顺序标号为(1..n)。接下来(m(mleq10^5))次询问,每次询问串(x)在串(y)中出现了几次。
Solution
首先根据(s_0)我们可以方便的建出一棵Trie树并建立fail指针,记录代表串(x)的节点为(end[x])。然后我们就得到了一个fail树:
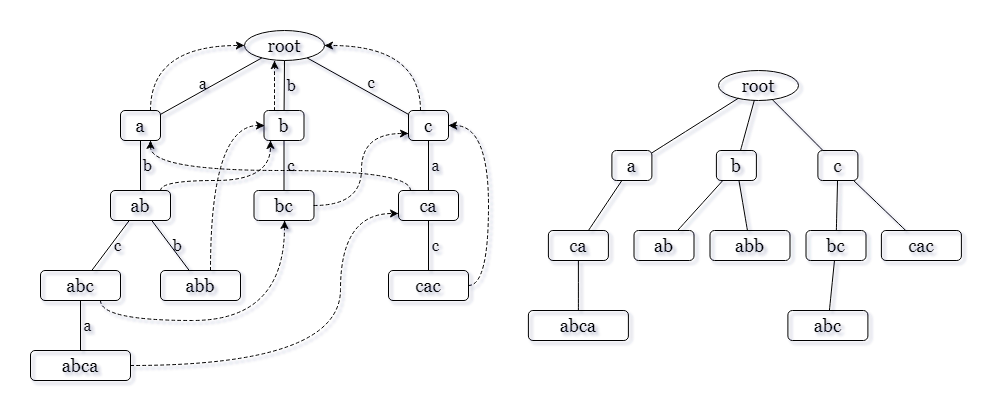
一个节点在fail树上的祖先就是它的一个后缀,子树就是以该节点作为后缀的串。那么询问就相当于“求(end[x])的子树中,有多少个点在(root)到(end[y])的路径上”。
我们求出fail树的DFS序,然后将询问按(y)排序。用树状数组维护每个点是否被标记,当(y)转移到(y+1)时,按照建立Trie树的方法转移。求(end[x])的子树中有多少个被标记的点就相当于求DFS序的区间和。
时间复杂度(O(nlogn+mlogn))。
Code
//[NOI2011]阿狸的打字机
#include <algorithm>
#include <cstdio>
using std::sort;
int const N=1e5+10;
int n; char s0[N];
struct query{int id,x,y,ans;} q[N];
bool cmpY(query x,query y) {return x.y<y.y;}
bool cmpID(query x,query y) {return x.id<y.id;}
int rt,ndCnt,fa[N],ch[N][26],fail[N]; int end[N];
int Q[N],op,cl;
int edCnt,h[N];
struct edge{int v,nxt;} ed[N];
void edAdd(int u,int v)
{
fail[v]=u;
edCnt++; ed[edCnt].v=v,ed[edCnt].nxt=h[u],h[u]=edCnt;
}
void bldFail()
{
for(int i=0;i<26;i++) ch[0][i]=rt;
Q[++cl]=rt;
while(op<cl)
{
int p=Q[++op];
for(int i=0;i<26;i++)
{
int q=ch[p][i];
if(!q) ch[p][i]=ch[fail[p]][i];
else edAdd(ch[fail[p]][i],q),Q[++cl]=q;
}
}
}
int dfCnt,fr[N],to[N];
void dfs(int u)
{
dfCnt++; fr[u]=dfCnt;
for(int i=h[u];i;i=ed[i].nxt) dfs(ed[i].v);
to[u]=dfCnt;
}
int tr[N];
void add(int x,int v) {while(x<=ndCnt) tr[x]+=v,x+=x&(-x);}
int sum(int x) {int r=0; while(x) r+=tr[x],x-=x&(-x); return r;}
int main()
{
scanf("%s",s0+1);
rt=++ndCnt;
for(int i=1,p=rt;s0[i];i++)
{
int x=s0[i]-'a';
if(s0[i]=='B') p=fa[p];
else if(s0[i]=='P') end[++n]=p;
else {if(!ch[p][x]) fa[ch[p][x]=++ndCnt]=p; p=ch[p][x];}
}
bldFail(); for(int i=1;i<=ndCnt;i++) if(!fr[i]) dfs(i);
int m; scanf("%d",&m);
for(int i=1;i<=m;i++) scanf("%d%d",&q[i].x,&q[i].y),q[i].id=i;
sort(q+1,q+m+1,cmpY);
int now=0,p=rt;
for(int i=0,owo=1,no;owo<=m;owo++)
{
int x=q[owo].x,y=q[owo].y;
while(now<y)
{
i++;
if(s0[i]=='B') add(fr[p],-1),p=fa[p];
else if(s0[i]=='P') now++;
else p=ch[p][s0[i]-'a'],add(fr[p],1);
}
q[owo].ans=sum(to[end[x]])-sum(fr[end[x]]-1);
}
sort(q+1,q+m+1,cmpID);
for(int i=1;i<=m;i++) printf("%d
",q[i].ans);
return 0;
}
P.S.
双倍经验BZOJ2434