论文提出了简单高效的PSS分支,仅需在原网络的基础上添加两个卷积层就能去掉NMS后处理,还能提升模型的准确率,而stop-grad的训练方法也挺有意思的,值得一看
来源:晓飞的算法工程笔记 公众号
论文: Object Detection Made Simpler by Eliminating Heuristic NMS

Introduction
当前主流的目标检测算法训练时大都一个GT对应多个正样本,使得推理时也会多个输出对应一个目标,不得不对结果进行NMS过滤。而论文的目标是设计一个简单的高性能全卷积网络,在不使用NMS情况下,能够进行完全的端到端训练。论文提出的方法十分简单,核心在于添加一个正样本选择分支(positive sample selector, PSS)。
论文的主要贡献如下:
- 检测流程在去掉NMS后变得更加简单,从FCOS到FCOS\(_{PSS}\)的修改能植入到其他的FCN解决方案中。
- 实验证明可以通过引入简单的PSS分支来代替NMS,植入FCOS仅需增加少量的计算量。
- PSS分支十分灵活,本质上相当于可学习的NMS,由于加入PSS分支没有影响到原有结构,可直接去掉PSS分支直接使用NMS。
- 在COCO上,得到与FCOS、ATSS以及最近的NMS-free方法相当或更好的结果。
- 提出的PSS分支可应用于其他anchor-based检测器中,在每个位置一个anchor box的设定下,仅通过PSS分支的动态训练样本选择也能达到不错的结果。
- 同样的想法也可用于其他目标识别任务中,如去掉实例分割中的NMS操作。
Our Method

FCOS\(_{PSS}\)的整体结构如图1所示,仅在FCOS的基础上添加了包含两个卷积层的SPP分支。
Overall Training Objective
完整的训练损失函数为:

\(\mathcal{L}_{fcos}\)为原版FCOS的损失项,包含分类损失、回归损失和center-ness损失。此外,还有PSS分支损失和ranking损失。在训练时\(\lambda_2\)设置为0.25,因为ranking损失对准确率只有些许提升。
-
PSS损失
PSS分支是NMS-free的关键,如图1所示,该分支的特征图输出为\(\mathbb{R}^{H\times W\times 1}\)。定义\(\sigma(pss)\)为特征图上的一个点,仅当该点为正样本时才设为1,所以可以把PSS分支当作二分类加入训练。但为了借用FCOS多分类的优势,论文将其与分类特征、center-ness特征进行融合:
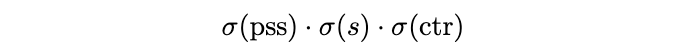
用上面的分数计算focal loss,与原本的FCOS分类的区别是,这里每个GT有且仅有一个正样本。
-
Ranking损失
论文通过实验发现,在训练时加入ranking损失能提升性能,ranking损失的定义为:

\(\gamma\)代表正负样本间的距离,默认设置为0.5。\(n_{+}\)和\(n_{-}\)为正负样本数量,\(\hat{P}_{i_{+}}(c_{i_{+}})\)为正样本\(i_{+}\)对应类别\(c_{i_{+}}\)的分类分数,\(\hat{P}_{i_{-}}(c_{i_{-}})\)为负样本\(i_{-}\)对应类别\(c_{i_{-}}\)的分类分数。在实验中,取top 100负样本分数进行计算。
One-to-many Label Assignment
一个GT选择多个anchor作为正样本进行训练是当前目标检测广泛采用的一种做法,这样的做法能够极大地简化标注要求,同时也能够兼容数据增强。即使标注位置有些许偏差,也不会改变选择的正样本。另外,多个正样本能够提供更丰富的特征,帮助训练更强大的分类器,比如尺寸不变性、平移不变性。因此,对于原生的FCOS分支的训练依然采用一对多的方式。
One-to-one Label Assignment
一对一的训练方式需要每次为GT选择最佳正样本,选择的时候需要考虑分类匹配程度和定位匹配程度,这里,先定义一个匹配分数\(Q_{i,j}\):

\(i\)为预测框编号,\(j\)为GT编号,超参数\(\alpha\)用来调整分类和定位间的比值。\(\Omega_j\)表示GT \(j\)的候选正样本,采用FCOS的规则,在GT的中心区域的点对应的anchor均为候选正样本。最后,对所有的GT及其正样本采用二分图匹配,通过匈牙利算法选择最大化\(\sum_{j}Q_{i,j}\)的匹配方案。
Conflict in the Two Classification Loss Terms
在论文提出的方案中,损失项\(\mathcal{L}_{fcos}\)采用一对多的匹配方案,而损失项\(\mathcal{L}_{pss}\)采用一对一的匹配方案,这意味着有部分anchor可能会被同时划分为正样本和负样本,导致模型难以收敛。为此,论文提出了stop-grad的概念,即阻止PSS分支的梯度回传到FCOS中。
Stop Gradient
stop-gradient操作在训练的时候将其中一部分网络设置为常数,定义\(\theta=\{\theta_{fcos},\theta_{pss}\}\)为网络需要优化的参数,训练的目标是求解:

将上述求解分成两个步骤:

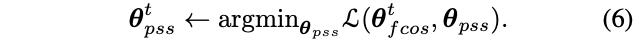
即在一轮迭代中,交替优化参数\(\theta_{fcos}\)和\(\theta_{pss}\)。比如在求解公式5时,\(\theta_{pss}\)的梯度置为零,按作者的说法,这块直接用pytorch的detach()进行分离。另外一种方法是直接分开训练,当求解公式5时,设置\(\theta_{pss}=0\)直到收敛,等同于原本的FCOS训练。而在训练PSS分支时,冻结FCOS参数直到收敛。论文通过实验发现分开训练可以极大地缩短训练时间,但性能稍差些。
Experiment
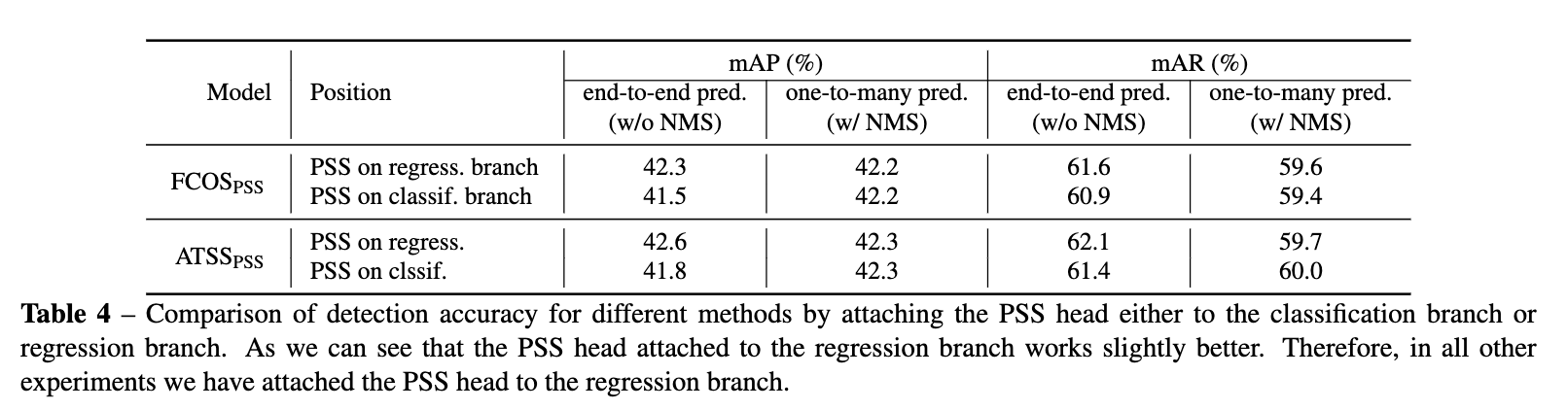
从论文的实验来看,PSS分支+stop grad的效果还是不错的。论文还有很大对比实验,有兴趣的可以去看看。
Conclusion
论文提出了简单高效的PSS分支,仅需在原网络的基础上添加包含两个卷积层就能去掉NMS后处理,还能提升模型的准确率,而stop-grad的训练方法也挺有意思的,值得一看。
如果本文对你有帮助,麻烦点个赞或在看呗~
更多内容请关注 微信公众号【晓飞的算法工程笔记】
