一、MATLAB绘制函数基础操作
1、plot( ):用于绘制二维的函数图形
(1)plot(x, y):绘制以x轴为横轴、y轴为纵轴的二维图形
(2)plot(x1, y1, x2, y2):在同一坐标性上绘制多组y-x二维图形
(3)plot(x, y, 'c'):参数c可以控制绘制的线条的属性,常用属性如下表:
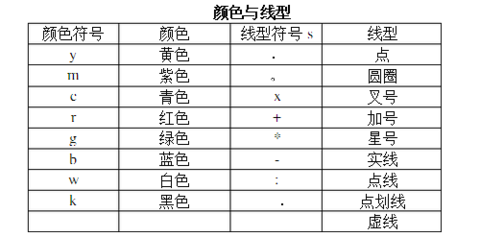
(4)plot3(x, y, z):用于绘制三维图形
(5)同类型的函数有:用于绘制二维脉冲图的steam(),绘制二维阶梯图的stairs()
2、subplot():建立子图轴系,在同一个Figure上同时绘制多个图形
(1)subplot(m,n,i):在同一个Figure上绘制m行n列的第i个图形
3、title():给图形添加标题
(1)title('string'):为图形添加标题'string'
(2)同类型函数有:为x轴添加标注的xlabel('string'),为y轴添加标注的ylabel('string')
4、axis():设定x轴y轴的长度
(1)axis([x_min, x_max, y_min, y_max]):设定x轴的大小为x_min到x_max,y轴的大小为y_min到y_max
二、MATLAB实践
1、矩阵操作:
1 A = [1 2 3; 4 5 6; 5 6 7]; % 声明一个矩阵A,用分号进行列的划分, 2 % 用空格或英文逗号划分列列中元素的 3 4 A(4, 2) = 1; % 直接对矩阵的元素进行赋值,注意下标索引是从1开始, 5 % 此时的矩阵被扩充为4*3 6 7 A(5, 1:3) = [-1 -2 -3]; % 对第5列的1到3元素进行相应的赋值 8 A([2, 5], : ) = []; % 第2列和第5列的整列元素赋值,[]表示清空 9 10 B = [1+2i, 3+4i; 5+6i, 7+8i]; % 声明复数矩阵 11 C = [1, 3; 5, 7] + [2, 4; 6, 8] * 1i; % 将复数i或j替换为1i或1j,以提高速度 12 E = C'; % 矩阵C的共轭转置 13 F = C.'; % 矩阵C的转置 14 G = conj(C); % 矩阵C的共轭 15 H = conj(C)'; % 矩阵C的共轭后的共轭转置,即转置 16 17 M = [1 3 5]; 18 N = [2 4 6]; 19 O = M + N; % 两个维数相同的矩阵可以直接相加 20 P = M - 2; % 矩阵M里的每个元素都减2 21 22 F1 = M * 3; % 矩阵里每个元素都乘上3 23 F2 = M.* N; % 矩阵M的每个元素乘上矩阵N里的对应元素,'.'点操作符指矩阵中的元素 24 F3 = M./N; % 矩阵M的每个元素除以矩阵N里的对应元素 25 F4 = M.N; % 矩阵N的每个元素除以矩阵M里的对应元素 26 F5 = M.^N;
2、函数绘制

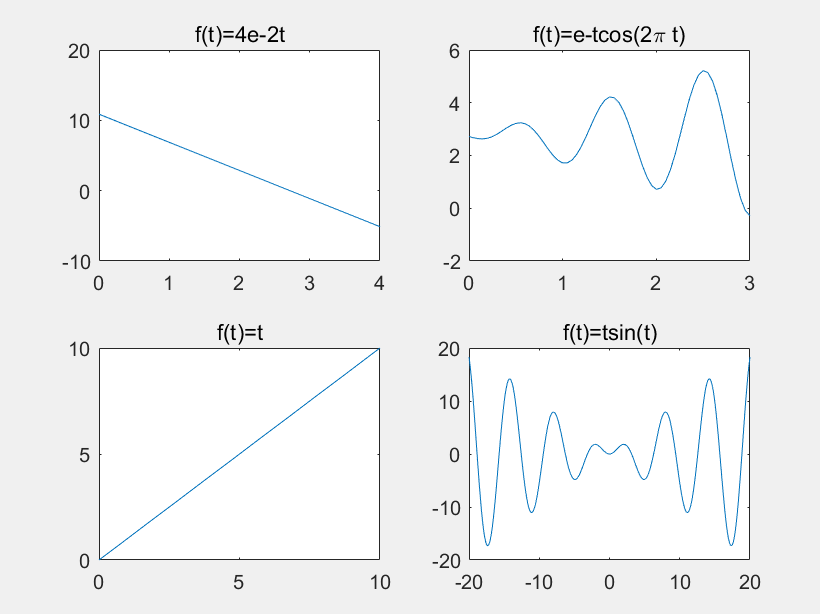
1 t1=0:0.05:4; 2 f1=-4*t1+4*exp(1); 3 t2=0:0.05:3; 4 f2=exp(1)-cos(2*pi*t2).*t2; % 注意这里需要使用数组乘法 5 t3=0:0.05:10; 6 f3=t3; 7 t4=-20:0.05:20; 8 f4=t4.*sin(t4); % 注意这里需要使用数组乘法 9 10 subplot(2,2,1), plot(t1, f1); 11 title('f(t)=4e-2t'); 12 subplot(2,2,2),plot(t2, f2); 13 title('f(t)=e-tcos(2pi t)'); 14 subplot(2,2,3), plot(t3, f3); 15 title('f(t)=t'); 16 subplot(2,2,4), plot(t4, f4); 17 title('f(t)=tsin(t)');
以上代码运行结果如下:
3、循环控制
1 X = 0; 2 for n = 1:20 3 X = X + (2*n - 1)^2; 4 end 5 6 Y = 0; 7 for n = 2:100 8 Y = Y + n*(n-1); 9 end 10 11 Z = zeros(1, 20); % 计算斐波那契数列前20项 12 Z(1, 1) = 1; 13 Z(1, 2) = 1; 14 for n = 3:20 15 Z(1, n) = Z(1, n-1) + Z(n-2); 16 end
