ZR最短路练习题

最短路的练习题

#257Div1B

题目传送

题意

给出一个N个节点的无向图，其中1是首都。
现在有两种边：
m条公路，每条连接两个节点，边权给出。
k条铁路，每条连接首都和另⼀个节点，边权给出。
问最多删去多少条铁路使得首都到任意节点的最
短路径长度不变。
(1 <= N,m,k <= 10^5.)

思路

• 首先说一下错误的贪心。
• 只按公路跑最短路，然后用铁路判断一下最短路是不是可以被再次更新
• 这样，可能造成，我们加上一条铁路，但是以后求的最短路数组可能再同过这条铁路更新，就错了
• 那么正解是什么啊？
• 既然单独把公路拿出来是不对的，那我们肯定要把铁路加进去求最短路
• 这时我们考虑到一个点的最短路，我们要取经过边数最多的那条
• 因为边数如果大于1就一定不用直达这个点的铁路了
• 如果它必须要用这条铁路，边数一定是1
• 还要注意的一点是如果有一条公路和铁路一模一样（起点也是1，边权相同且是最短，那这条铁路是不必要的
• 所以我们只需判断那条铁路是必要的，最后取补集就好

Bug

• 数组开小
• spfa死了
• diji写挂了，pair里第一维是距离dis,第二维是序号
• 我**写反了，导致了MLE的好成绩

代码

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<queue>
#include<vector>
#define M 300005
#define N 100005
#define ll long long 
using namespace std;
int n,m,k,res,tot;
int head[N],tep[N],d[N],po[N];
ll dis[N];
typedef pair<ll,int> pll;
struct node{
	int to,net,val;
}e[1000005];
priority_queue<pll,vector<pll>,greater<pll> >q;
void add(int x,int y,int z){
	e[++tot].to =y;
	e[tot].val =z;
	e[tot].net =head[x];
	head[x]=tot;
}
inline int read(){
	int s=0,w=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
	while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
	return s*w;
}
void SPFA(){
	for(int i=1;i<=n;i++) dis[i]=1e17;
	dis[1]=0;
	q.push(make_pair(0,1));
	while(!q.empty()){
		int u=q.top().second;
		if(q.top().first!=dis[u]){
			q.pop();continue;
		}
		q.pop();
		for(int i=head[u];i;i=e[i].net ){
			int to=e[i].to ;
			if(dis[to]>dis[u]+e[i].val ){
				dis[to]=dis[u]+e[i].val ;
				d[to]=d[u]+1;
				q.push(make_pair(dis[to],to));
			}
			else if(dis[to]==dis[u]+e[i].val&&d[to]<d[u]+1){
				d[to]=d[u]+1;
				q.push(make_pair(dis[to],to));
			}
		}
	}
}
int main(){
	n=read();m=read();k=read();
	for(int i=1;i<=m;i++){
		int a,b,c;
		a=read();b=read();c=read();
		add(a,b,c);
		add(b,a,c);
		if(a==1){
			if(po[b]==0) po[b]=c;
			else po[b]=min(po[b],c);
		}
		if(b==1){
			if(po[a]==0) po[a]=c;
			else po[a]=min(po[a],c);
		} 
	}
	for(int i=1;i<=k;i++){
		int a,b;
		a=read();b=read();
		add(1,a,b);
		if(tep[a]!=0) tep[a]=min(tep[a],b);
		else tep[a]=b;
	}
	SPFA();//(sizeof(head)>>20)+(sizeof(po)>>20)+(sizeof(tep)>>2
//	printf("%d 
",sizeof(e)>>20);
	for(int i=2;i<=n;i++)
	  if(d[i]==1){
		if(dis[i]==tep[i]&&po[i]!=dis[i]) res++;  
	}
	printf("%d",k-res);
	return 0;
} 

小结

• 经过最多条边的最短路 ，记录条数，每次松弛时更新

Edu 38 D

题目传送

题意

给出一个 (N) 个点 (M) 条边的无向图。
定义 (d(i,j)) 为两点间最短路的长度。 每个点定义了点权 (a_i) 。
现在对于图中的每个点i，你都需要计算

[minlimits_{j=1}^{n} lbrace2cdot dis(i,j)+a_j brace ]

(1 leqslant N,M leqslant10^5)

思路

• 这个式子看起来不像最短路
• 是因为后边有个点权 (a_i)
• 我们把它变个形式
• (dis(0,j)=a_j)
• 这不就变成了最短路形式的式子了吗
• 可以发现前边的乘2完全没有影响，我们只要把边权乘个系数就行
• 加个超级源点
• 从超级源点到每个点连边，边权是这个点的点权
• 然后我们从超级源点跑一遍单源最短路就行了

代码

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<queue>
#define N 200005
#define ll long long 
#define MP make_pair
using namespace std;
typedef pair<ll,int> pll;
struct node{
	int to,net;
	ll  val;
}e[1000005];
int n,m,tot;
int head[N];
ll dis[N];
priority_queue<pll,vector<pll>,greater<pll> >q;
void add(int x,int y,ll z){
	e[++tot].to =y;
	e[tot].val=z;
	e[tot].net =head[x];
	head[x]=tot;
}
void SPFA(){
	for(int i=0;i<=n;i++) dis[i]=1e17;
	dis[0]=0;
	q.push(MP(0,0));
	while(!q.empty()){
		int u=q.top().second;
		if(dis[u]!=q.top().first){
			q.pop();
			continue;
		}
		q.pop();
		for(int i=head[u];i;i=e[i].net ){
			int to=e[i].to ;
			if(dis[to]>dis[u]+e[i].val ){
				dis[to]=dis[u]+e[i].val;
				q.push(MP(dis[to],to));
			}
		}
	}
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++){
		int a,b;ll c;
		scanf("%d%d%lld",&a,&b,&c);
		c*=2;
		add(a,b,c);
		add(b,a,c);
	}
	for(int i=1;i<=n;i++){
		ll x;
		scanf("%lld",&x);
		add(0,i,x);
	}
	SPFA();
	for(int i=1;i<=n;i++) printf("%lld ",dis[i]);
	return 0;
}

小结

• 建超级源点

HDU4479（边权递增最短路

题目传送

题意

无向图求 (1->N) 的边权递增的最短路。边权应严格单调递增

思路

• 如果不要求严格递增，也就是边权都不相同
• 那么只需按边权排序，从小到大松弛即可
• 如果要求严格递增
• 我们在原来的基础上，考虑那些边权相同的边我们并不能一条一条的顺序跟新 (dis) 数组
• 因为这样就可能有边权相同的同时被加入
• 那么我们考虑同时处理这些边，每次松弛都用上上一种边权的 (dis) 来更新，来保证它没有相同边权的边同时加入

Bug

• 在把一堆边松弛后更新 (dis) 时，要取个最小值，而不是直接赋值
• 因为有可能出现这种情况
• 

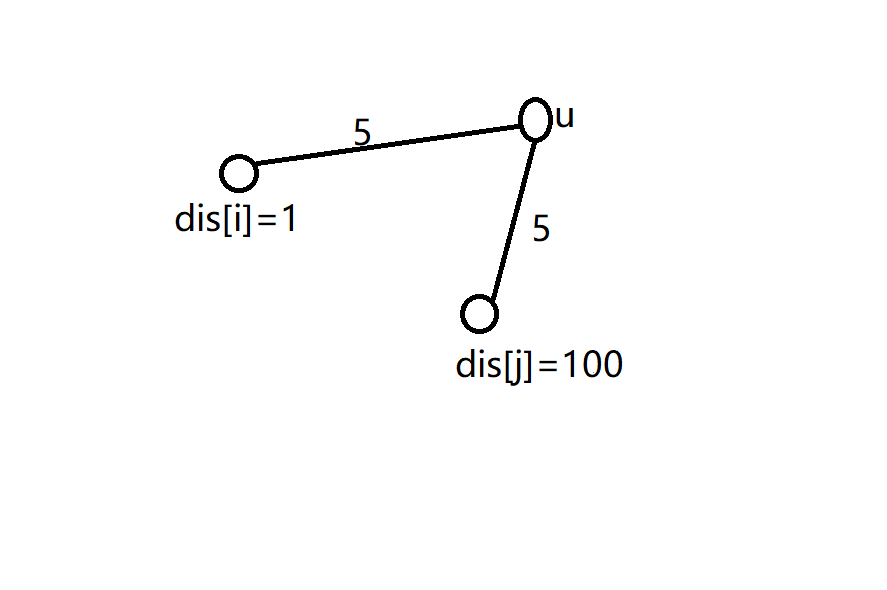
就是边权相同的边先后更新 (dis)

小结

• 边权递增最短路，按边权从小到大的顺序依次松弛，边权相等的要一起松弛

代码

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<queue>
#include<vector>
#define N 10005
#define M 50005
#define ll long long
using namespace std;
int T,n,m,tot;
//vector<pair<ll,int> > ton;
struct node{
	int to,net,val;
}e[M<<1];
struct Edge{
	int x,y,z;
}q[M];
struct Now{
	int to;
	ll val;
}ton[M];
int head[N],pre[N];
ll dis[N];
bool cmp(Edge a,Edge b){
	return a.z<b.z ;
}
inline int read(){
	int s=0,w=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
	while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
	return s*w;
}
int main()
{
	T=read();
	while(T--){
		n=read();m=read();
		for(int i=1;i<=n;i++) dis[i]=1e17;
		dis[1]=0;
		for(int i=1;i<=m;i++)
			q[i].x =read(),q[i].y =read(),q[i].z =read();
		sort(q+1,q+m+1,cmp);
		int last=0,cnt=1,res=0;
		while(cnt<=m){
			int u,v,w;
			u=q[cnt].x ,v=q[cnt].y ,w=q[cnt].z ;
			if(w!=last){
				for(int i=1;i<=res;i++) dis[ton[i].to]=min(dis[ton[i].to],ton[i].val);
				last=w;
				res=0;
//				cout<<"Debug"<<endl;
		    }
			if(dis[v]>dis[u]+w) ++res,ton[res].val=dis[u]+w,ton[res].to =v;
			if(dis[u]>dis[v]+w) ++res,ton[res].val=dis[v]+w,ton[res].to =u;
//			cout<<"Debug"<<endl;
			cnt++;
			
		}
		for(int i=1;i<=res;i++) dis[ton[i].to]=ton[i].val;
//		for(int i=1;i<=n;i++) printf("%d ",dis[i]);
//		cout<<endl;
		if(dis[n]==1e17) printf("No answer
");
		else printf("%I64d
",dis[n]);
	}
	return 0;
} 

CF#416E

题目传送

题意

求任意点对 ((i,j)) 求出 ((i,j)) 最短路中覆盖边数
(n<500)

思路

• 我们首先能给出一个 (O(n^4)) 的暴力
• 求多源最短路
• 枚举点对，枚举每一条边，看这条边是否在最短路上
• 考虑枚举点对后，再枚举边会超时，但枚举点却不会
• 所以我们枚举在最短路上的点
• 如果这个点 (u) 在 ((s,t)) 最短路上
• 应满足 $$f[s][t]=f[s][u]+f[u][t]$$
• 对于在最短路上的这个点 (u)，我们只要求出 (s) 到这个点 (u) 的最短路上以 (u) 为结尾的最短路上的边数
• 我们可以枚举点 (s)
• 再枚举边，看这条边是否在最短路上，按照前边的朴素算法的判断方法
• 如果这条边是最短路上的边，那么在端点的计数器上++，还要记录起点是什么，所有要用二维的计数器

Bug

• 注意二维的计数器的大小，不然MLE ,RE

小结

• 最短路经典问题:求最短路的覆盖边数，改动弗洛伊德，枚举中间点，预处理

代码

#include<iostream>
#include<algorithm>
#include<cstdio>
#define ll long long 
using namespace std;
int e[505][505];
int res[505][505];
int n,m;
int ans;
struct node{
	int from,to,val;
}d[250005];
int  main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++){
		int a,b,c;
		scanf("%d%d%d",&a,&b,&c);
		e[a][b]=c;
		e[b][a]=c;
		d[i].from =a,d[i].to =b,d[i].val=c;
	}
	for(int i=1;i<=n;i++)
	  for(int j=1;j<=n;j++){
	  	if(!e[i][j]) e[i][j]=1e9+7;
	  	if(i==j) e[i][j]=0;
	  }
	for(int k=1;k<=n;k++)
	  for(int i=1;i<=n;i++)
	    for(int j=1;j<=n;j++)
	      e[i][j]=min(e[i][j],e[i][k]+e[k][j]);
//	for(int i=1;i<=n;i++){
//		for(int j=1;j<=n;j++) printf("%d ",e[i][j]);
//		cout<<endl;
//	}
	for(int i=1;i<=n;i++)
	  for(int j=1;j<=m;j++){
	  	if(e[i][d[j].from]+d[j].val==e[i][d[j].to])	res[i][d[j].to]++;
	  	if(e[i][d[j].to]+d[j].val==e[i][d[j].from]) res[i][d[j].from ]++;
	  }
	for(int u=1;u<=n;u++)
	  for(int v=u+1;v<=n;v++){
	  	ans=0;
	  	for(int i=1;i<=n;i++)
	  	  if(e[u][i]+e[i][v]==e[u][v]) ans+=res[u][i];
	  	printf("%d ",ans);
	  }
	return 0;
} 

赛前模拟题

link

思路

• 考虑Floyd。
• 按点权排序，跑Floyd，顺便记录一下中间点。也就是用点权小于一个值的点跑的最短路

代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#define N 205
#define M 20004
using namespace std;
int T,n,m;
int f[N][N][N],e[N][N];
struct node{
    int id,val;
}d[N];
struct query{
    int s,t,w,as,id;
}Q[M];
bool cmp1(node a,node b){
    return a.val<b.val;
}
bool cmp2(query a,query b){
    return a.w<b.w;
}
bool cmp3(query a,query b){
    return a.id<b.id;
}
//inline int read(){
//  int s=0,w=1;char ch=getchar();
//  while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
//  while(ch>='0'&&ch<='9'){s=s*10+ch-'0',ch=getchar();}
//  return s*w;
//}
struct ios {
    inline char gc(){
        static const int IN_LEN=1<<18|1;
        static char buf[IN_LEN],*s,*t;
        return (s==t)&&(t=(s=buf)+fread(buf,1,IN_LEN,stdin)),s==t?-1:*s++;
    }
  
    template <typename _Tp> inline ios & operator >> (_Tp&x){
        static char ch,sgn; ch = gc(), sgn = 0;
        for(;!isdigit(ch);ch=gc()){if(ch==-1)return *this;sgn|=ch=='-';}
        for(x=0;isdigit(ch);ch=gc())x=x*10+(ch^'0');
        sgn&&(x=-x); return *this;
    }
} io;
int main(){
//  freopen("C.in","r",stdin);
//  freopen("C.out","w",stdout);
//  T=read();
    io>>T;
    while(T--){
        io>>n;
        io>>m;
//      n=read();m=read();
        for(int i=1;i<=n;i++) io>>d[i].val,d[i].id=i;
        for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++) io>>f[i][j][0],e[i][j]=f[i][j][0];
        for(int i=1;i<=m;i++){
            io>>Q[i].s;
            io>>Q[i].t;
            io>>Q[i].w;
//          Q[i].s=read();
//          Q[i].t=read();
//          Q[i].w=read();
            Q[i].id=i;
        }
        sort(d+1,d+n+1,cmp1);
        sort(Q+1,Q+m+1,cmp2);
        for(register int k=1;k<=n;k++){
            for(register int i=1;i<=n;i++)
              for(register int j=1;j<=n;j++)
                if(e[i][j]>e[i][d[k].id]+e[d[k].id][j])
                    e[i][j]=e[i][d[k].id]+e[d[k].id][j];
            for(register int i=1;i<=n;i++)
              for(register int j=1;j<=n;j++) f[i][j][k]=e[i][j]; 
        }
        int cnt=1;
        for(int i=1;i<=m;i++){
            while(Q[i].w>=d[cnt].val&&cnt<=n) cnt++;
            Q[i].as=f[Q[i].s][Q[i].t][cnt-1];
        }
        sort(Q+1,Q+m+1,cmp3);
        for(int i=1;i<=m;i++) printf("%d
",Q[i].as); 
    }
    return 0;
}

ZR普转提Day6D

LINK