L - Common Subsequence POJ - 1458
题目链接:https://vjudge.net/contest/68966#problem/L
题目:
给定序列的子序列是给定序列,其中省略了一些元素(可能没有)。给定序列X = <x1,x2,...,xm>另一个序列Z = <z1,z2,...,zk>是X的子序列,如果存在严格增加的序列<i1,i2,..对于所有j = 1,2,...,k,x ij = zj,X的索引,...,ik>。例如,Z = <a,b,f,c>是X = <a,b,c,f,b,c>的子序列,其索引序列<1,2,4,6>。给定两个序列X和Y,问题是找到X和Y的最大长度公共子序列的长度。
输入
程序输入来自std输入。输入中的每个数据集包含两个表示给定序列的字符串。序列由任意数量的空格分隔。输入数据是正确的。
产量
Sample Input
abcfbc abfcab programming contest abcd mnpSample Output
4 2 0
思路:通过这个去看了下LCS:
LCS是Longest Common Subsequence的缩写,即最长公共子序列。一个序列,如果是两个或多个已知序列的子序列,且是所有子序列中最长的,则为最长公共子序列。
比如,对于char x[]="aabcd";有顺序且相互相邻的aabc是其子序列,有顺序但是不相邻的abc也是其公共子序列。即,只要得出序列中各个元素属于所给出的数列,就是子序列。
再加上char y[]="12abcabcd";对比出才可以得出最长公共子序列abcd。
在两个字符串中,有些字符会一样,可以形成的子序列也有可能相等,因此,长度最长的相等子序列便是两者间的最长公共字序列,其长度可以使用动态规划来求。
以s1={1,3,4,5,6,7,7,8},s2={3,5,7,4,8,6,7,8,2}为例。
借用《算法导论》中的推导图:
创建 DP数组C[][];
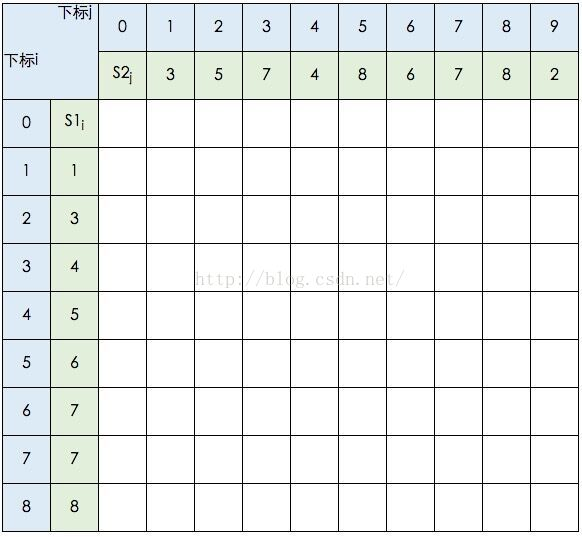
图中的空白格子需要填上相应的数字(这个数字就是c[i][j]的定义,记录的LCS的长度值)。填的规则依据递归公式,简单来说:如果横竖(i,j)对应的两个元素相等,该格子的值 = c[i-1,j-1] + 1。如果不等,取c[i-1,j] 和 c[i,j-1]的最大值。首先初始化该表:
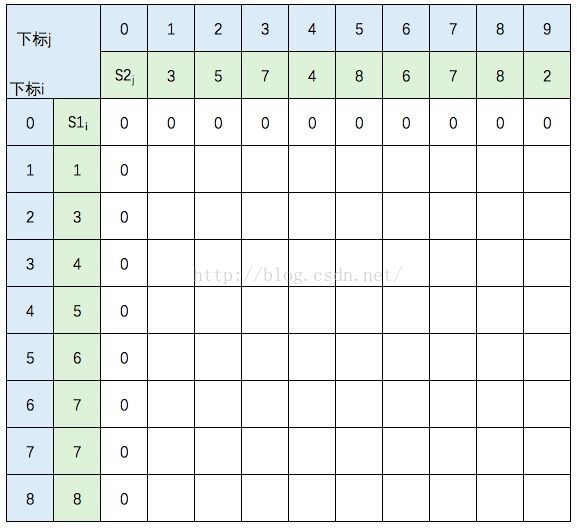
然后,一行一行地从上往下填:
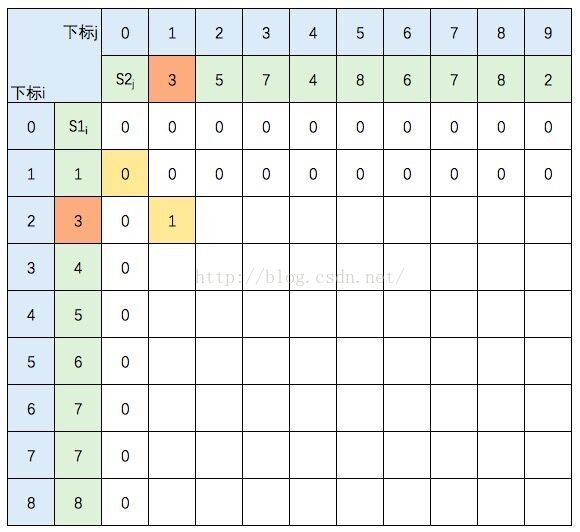
S1的元素3 与 S2的元素3 相等,所以 c[2,1] = c[1,0] + 1。继续填充:
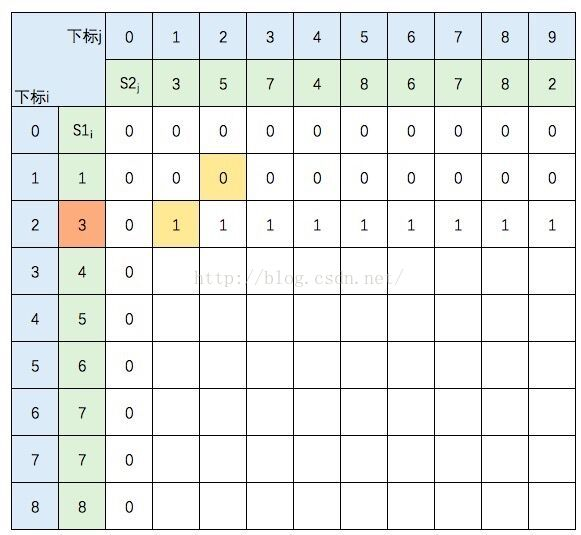
S1的元素3 与 S2的元素5 不等,c[2,2] =max(c[1,2],c[2,1]),图中c[1,2] 和 c[2,1] 背景色为浅黄色。
继续填充:
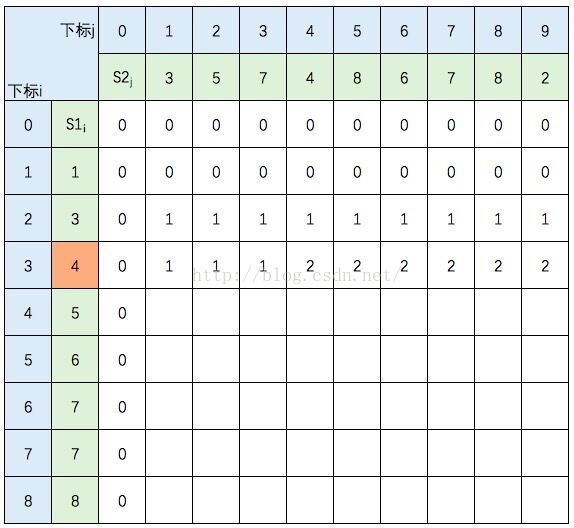
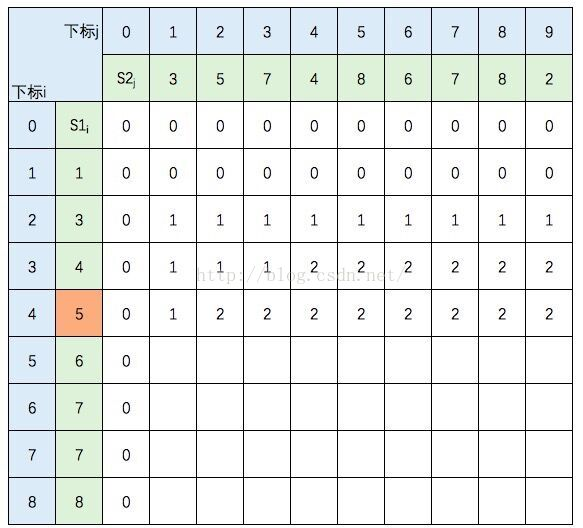
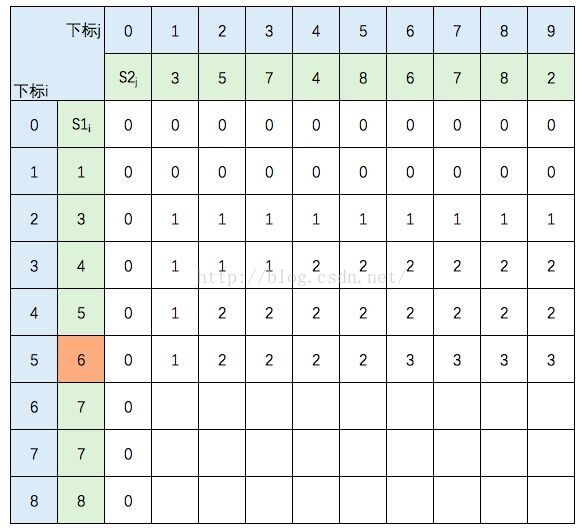
中间几行填写规则不变,直接跳到最后一行:

至此,该表填完。根据性质,c[8,9] = S1 和 S2 的 LCS的长度,即为5。
得到公式

LCS代码如下(也是该题AC代码):
以s1={1,3,4,5,6,7,7,8},s2={3,5,7,4,8,6,7,8,2}为例。
借用《算法导论》中的推导图:
创建 DP数组C[][];

图中的空白格子需要填上相应的数字(这个数字就是c[i][j]的定义,记录的LCS的长度值)。填的规则依据递归公式,简单来说:如果横竖(i,j)对应的两个元素相等,该格子的值 = c[i-1,j-1] + 1。如果不等,取c[i-1,j] 和 c[i,j-1]的最大值。首先初始化该表:

然后,一行一行地从上往下填:

S1的元素3 与 S2的元素3 相等,所以 c[2,1] = c[1,0] + 1。继续填充:

S1的元素3 与 S2的元素5 不等,c[2,2] =max(c[1,2],c[2,1]),图中c[1,2] 和 c[2,1] 背景色为浅黄色。
继续填充:



中间几行填写规则不变,直接跳到最后一行:

至此,该表填完。根据性质,c[8,9] = S1 和 S2 的 LCS的长度,即为5。
得到公式

LCS代码如下(也是该题AC代码):
//
// Created by hanyu on 2019/8/8.
//
#include <algorithm>
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#include <set>
#include<math.h>
#include<map>
using namespace std;
typedef long long ll;
const int maxn=1000+7;
#define MAX 0x3f3f3f3f
int main()
{
char s[maxn],s1[maxn];
int dp[maxn][maxn];
while(~scanf("%s%s",s,s1))
{
int n=strlen(s);
int n1=strlen(s1);
memset(dp,0,sizeof(dp));
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n1;j++)
{
if(s[i-1]==s1[j-1])
dp[i][j]=dp[i-1][j-1]+1;
else
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
}
}
printf("%d
",dp[n][n1]);
}
return 0;
}