\(0.\)解决问题
在树状数组那篇博客中,留下了一个坑:
区间修改区间查询
今天我们就要来解决这个问题
\(1.\)前置知识
二分
二叉树
都很简单
\(2.\) 简介
线段树是一种可以较快维护满足区间可加性区间信息(如:区间和,区间积,区间最大最小等)的数据结构,其基本思想就是二分。
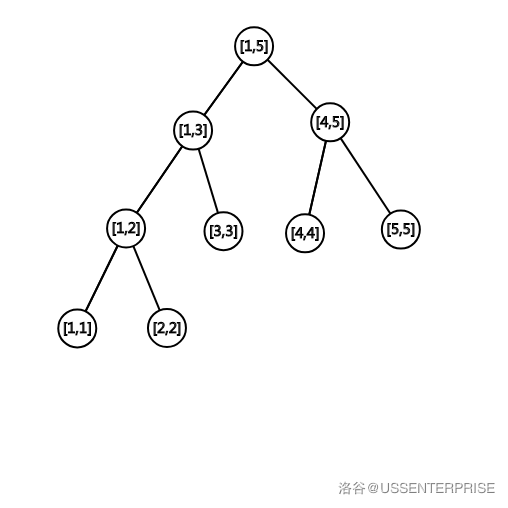
注:区间可加性指一些可以通过子区间信息合并维护的信息,如区间最大就可以由二分后两个子区间最大值得到
\(3.\) 基本操作(以区间加和为例,无优化)
约定
以下代码运用到的宏和全局变量及其解释:
#define ls now<<1
#define rs now<<1|1
建树
对于一棵线段树,我们可以递归地建树。根据二分的思想,我们可以每次进行二分,分别建立左子树和右子树,直到递归到叶子结点(即\(l=r\))
- pushup操作
pushup操作是用来合并子区间信息的操作,对于区间加和,此操作所干的事就是\(sumv_{[l,r]}=sumv_{[l,mid]}+sumv_{[mid+1,r]}\)
建树代码如下:
inline void pushup(int now){ sumv[now]=sumv[ls]+sumv[rs]; }
inline void build(int now,int l,int r){
if(l==r){ sumv[now]=a[l]; return;}
rg int mid=(l+r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
pushup(now);
}
单点修改
其实完全不用这样维护
基本思想:二分查找
代码:
inline void change(int now,int l,int r,int x,int v){
if(l==r){ sumv[now]=v; return; }
rg int mid=(l+r)>>1;
if(x<=mid) change(ls,l,mid,x,v);
else change(rs,mid+1,r,x,v);
pushup(now);
}
区间修改
二行版
思想:对于一个想要修改的区间\([ql,qr]\),假设你现在到了编号为\(now\)的节点,其管控的区间为\([l,r]\),中点为\(mid\),如果\(ql \leq mid\)则证明修改区间与\([l,mid]\)有相交的部分,需修改左半区间;同理,如果\(mid<qr\),则需修改右区间(如下图)
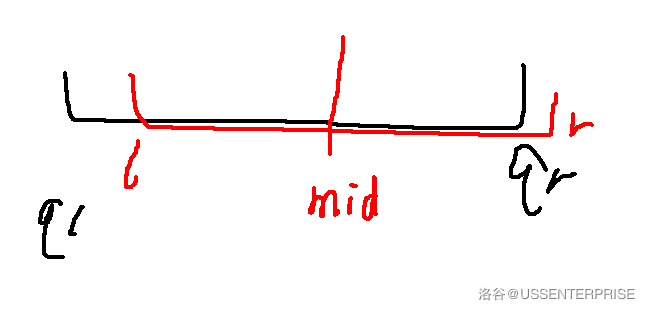
代码如下:
inline void change(int now,int l,int r,int ql,int qr,int v){
if(l==r){ sumv[now]+=v; return; }
int mid=(l+r)>>1;
if(ql<=mid) change(ls,l,mid,ql,qr,v);
if(mid<qr) change(rs,mid+1,r,ql,qr,v);
pushup(now);
}
三行版
思想:对于一个想要修改的区间\([ql,qr]\),假设你现在到了编号为\(now\)的节点,其管控的区间为\([l,r]\),中点为\(mid\),如果\(ql>mid\),则证明所需修改的区间全部位于右半区间及其以右,修改右区间;同理,如果\(qr\leq mid\),需修改右区间。额外的,其他情况则证明修改区间左右兼占,需修改两个区间(如下图)
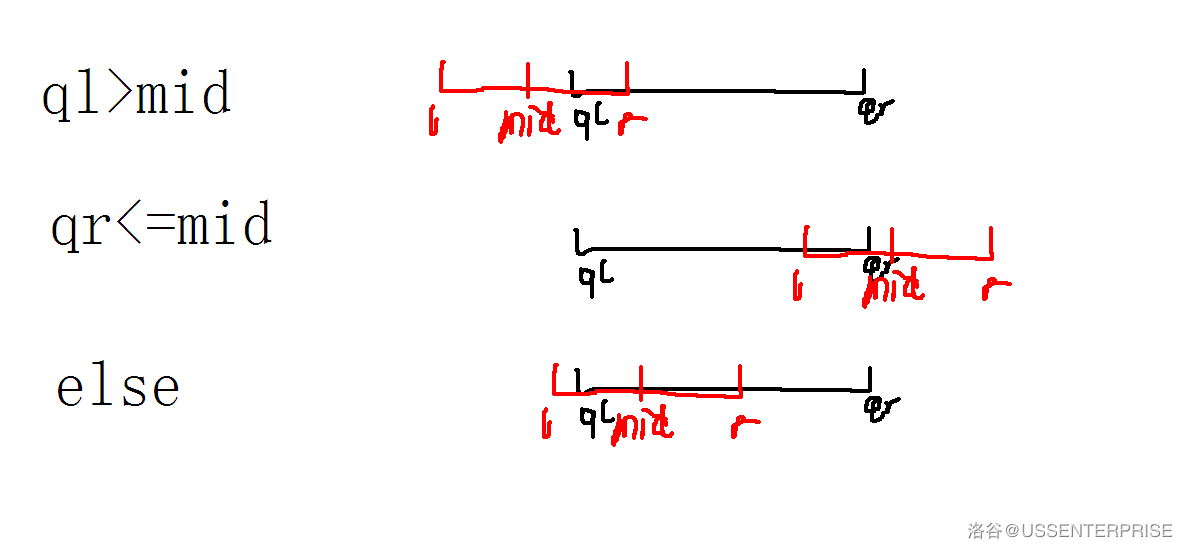
inline void optadd(int now,int l,int r,int ql,int qr,int v){
if(l==r){ sumv[now]+=v; return; }
rg int mid=(l+r)>>1;
if(ql>mid) optadd(rs,mid+1,r,ql,qr,v);
else if(qr<=mid) optadd(ls,l,mid,ql,qr,v);
else optadd(ls,l,mid,ql,qr,v),optadd(rs,mid+1,r,ql,qr,v);
}
注:请注意二行版与三行版关于情况之间关系的不同
区间查询
思想:对于一个查询区间\([ql,qr]\),为了节省时间,只需递归到一个包含于此区间的区间\([l_i,r_i]\)即可。\(ans=\sum[l_i,r_i]\)
注:二行版和三行版思想与上方相同,下同,不再解释
//二行版
inline int query(int now,int l,int r,int ql,int qr){
if(ql<=l&&r<=qr) return sumv[now];
rg int mid=(l+r)>>1,ans=0;
if(ql<=mid) ans+=query(ls,l,mid,ql,qr);
if(mid<qr) ans+=query(rs,mid+1,r,ql,qr);
return ans;
}
//三行版
inline int query(int now,int l,int r,int ql,int qr){
if(ql<=l&&r<=qr) return sumv[now];
rg int mid=(l+r)>>1,ans=0;
if(ql>mid) ans=query(rs,mid+1,r,ql,qr,v);
else if(qr<=mid) ans=query(ls,l,mid,ql,qr,v);
else ans=query(ls,l,mid,ql,qr,v)+query(rs,mid+1,r,ql,qr,v);
return ans;
}
\(4.\) 线段树的基本优化(\(lazy\)标记)
可以发现,我们在区间修改这一环节时间开销比较大,每次修改都需要递归到叶子结点才可以完成。但是查询时并不需要查找每个叶子节点的值
所以懒惰的人类就有了\(lazy\)标记这种做法
我们只需要在每次修改时为区间打上一个标记,在需要查询叶子结点时再将标记和修改下放一层,就可以以较小的时间开销完成修改。
\(pushdown\)操作
\(pushdown\)操作就是完成上述下放标记的一个操作。首先,很显然的一点是如果当前节点不存在任何标记,我们就不需要对其下放。
代码如下
inline void pushdown(int o,int l,int r){
if(addv[o]==0) return;
lazy[o<<1]+=lazy[o];
lazy[o<<1|1]+=lazy[o];
int mid=(l+r)>>1;
sumv[o<<1]+=lazy[o]*(mid-l+1);
sumv[o<<1|1]+=lazy[o]*(r-mid);
lazy[o]=0;
}
注:下放标记后必须清零,因为如果不清零,当前区间就相当于多加了一个标记。
\(change,query\)优化后的做法。
优化后的查询(\(query\))操作只需在原有代码递归前进行标记下方即可
优化后的修改操作(\(change\))基本形式和查询十分相似,具体见代码
\(5.\) 例题
思路:权值线段树+树上二分查找区间第k大
思路:标记活用或同时维护区间和和区间最大+单点修改\最大树与求和树同时维护
思路:二叉树经典例题,也可以用线段树解决