poj 2046 Gap（bfs+hash）

Description

Let's play a card game called Gap. 
You have 28 cards labeled with two-digit numbers. The first digit (from 1 to 4) represents the suit of the card, and the second digit (from 1 to 7) represents the value of the card. 

First, you shu2e the cards and lay them face up on the table in four rows of seven cards, leaving a space of one card at the extreme left of each row. The following shows an example of initial layout. 

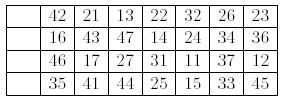
Next, you remove all cards of value 1, and put them in the open space at the left end of the rows: "11" to the top row, "21" to the next, and so on. 

Now you have 28 cards and four spaces, called gaps, in four rows and eight columns. You start moving cards from this layout. 

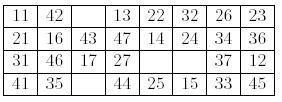
At each move, you choose one of the four gaps and fill it with the successor of the left neighbor of the gap. The successor of a card is the next card in the same suit, when it exists. For instance the successor of "42" is "43", and "27" has no successor. 

In the above layout, you can move "43" to the gap at the right of "42", or "36" to the gap at the right of "35". If you move "43", a new gap is generated to the right of "16". You cannot move any card to the right of a card of value 7, nor to the right of a gap. 

The goal of the game is, by choosing clever moves, to make four ascending sequences of the same suit, as follows. 

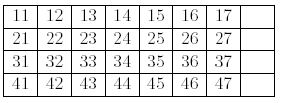
Your task is to find the minimum number of moves to reach the goal layout.

Input

The input starts with a line containing the number of initial layouts that follow. 

Each layout consists of five lines - a blank line and four lines which represent initial layouts of four rows. Each row has seven two-digit numbers which correspond to the cards. 

Output

For each initial layout, produce a line with the minimum number of moves to reach the goal layout. Note that this number should not include the initial four moves of the cards of value 1. If there is no move sequence from the initial layout to the goal layout, produce "-1".

Sample Input

4

12 13 14 15 16 17 21
22 23 24 25 26 27 31
32 33 34 35 36 37 41
42 43 44 45 46 47 11

26 31 13 44 21 24 42
17 45 23 25 41 36 11
46 34 14 12 37 32 47
16 43 27 35 22 33 15

17 12 16 13 15 14 11
27 22 26 23 25 24 21
37 32 36 33 35 34 31
47 42 46 43 45 44 41

27 14 22 35 32 46 33
13 17 36 24 44 21 15
43 16 45 47 23 11 26
25 37 41 34 42 12 31

Sample Output

0
33
60
-1

Source

Japan 2003,Aizu

 

这题的关键在用hash来保存状态，其他的是bfs基础了。。。

 

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
#include<stdlib.h>
using namespace std;
#define M 1000007
#define ll long long
ll aimNum;
ll hash[M];
struct Node{
    ll x[5],y[5];//存空格的横纵坐标
    ll mp[6][9];//存整张地图
    long long time;//存时间
}tmp;
ll flag;
ll aim[6][9]={
    11,12,13,14,15,16,17,0,
    21,22,23,24,25,26,27,0,
    31,32,33,34,35,36,37,0,
    41,42,43,44,45,46,47,0
};
ll base[33]={1};

bool inserNum(ll ans){//hash的插入，看看是否跟之前的状态相同，其实跟vis数组标记一个意思
    ll val=ans%M;
    while(hash[val]!=-1 && hash[val]!=ans){
        val=(val+10)%M;
    }
    if(hash[val]==-1){
        hash[val]=ans;
        return true;//可以插入返回true
    }
    return false;//否则返回false
}

bool work(Node cnt){
    ll ans=0;
    for(ll i=0;i<4;i++){
        for(ll j=0;j<8;j++){
            ans=ans+cnt.mp[i][j]*base[i*8+j];//ans为整张图的hash值
        }
    }
    if(ans==aimNum){
        flag=1;
    }
    if(inserNum(ans))
        return true;
    return false;
}

ll bfs(){
    queue<Node>q;
    q.push(tmp);
    Node t1,t2;
    while(!q.empty()){
        t1=q.front();
        q.pop();

        for(ll k=0;k<4;k++){//4个空格依次遍历
            t2=t1;
            ll tx=t2.x[k];
            ll ty=t2.y[k];
            for(ll i=0;i<4;i++){//遍历整张图，寻找符合的数
                for(ll j=0;j<8;j++){
                    if(t2.mp[i][j]==0) continue;//如果要调换的还是空格，则不行
                    if(t2.mp[i][j]!=t2.mp[tx][ty-1]+1) continue;//需要填入的数为前一个+1


                    swap(t2.mp[i][j],t2.mp[tx][ty]);
                    if(work(t2)){//判断是否可以继续往下走
                        t2.time=t1.time+1;
                        t2.x[k]=i;//将新的空格的横纵坐标保存下来
                        t2.y[k]=j;
                        q.push(t2);
                        if(flag)
                            return t2.time;
                    }

                }
            }
        }
    }
    return -1;
}
int main()
{

    for(ll i=1;i<33;i++){
        base[i]=base[i-1]*2;
    }
    aimNum=(ll)98430874871;//aimNum是通过事先计算得出的

    int t;
    scanf("%d",&t);

    while(t--){

        memset(hash,-1,sizeof(hash));

        tmp.mp[0][0]=tmp.mp[1][0]=tmp.mp[2][0]=tmp.mp[3][0]=0;

        int k=0;
        for(int i=0;i<4;i++){
            for(int j=1;j<8;j++){
                scanf("%I64d",&tmp.mp[i][j]);

                if(tmp.mp[i][j]==11) {
                    swap(tmp.mp[i][j],tmp.mp[0][0]);
                    tmp.x[k]=i;
                    tmp.y[k++]=j;
                }
                if(tmp.mp[i][j]==21) {
                    swap(tmp.mp[i][j],tmp.mp[1][0]);
                    tmp.x[k]=i;
                    tmp.y[k++]=j;
                }
                if(tmp.mp[i][j]==31) {
                    swap(tmp.mp[i][j],tmp.mp[2][0]);
                    tmp.x[k]=i;
                    tmp.y[k++]=j;
                }
                if(tmp.mp[i][j]==41) {
                    swap(tmp.mp[i][j],tmp.mp[3][0]);
                    tmp.x[k]=i;
                    tmp.y[k++]=j;
                }
            }
        }

        tmp.time=0;//时间初始化为0
        flag=0;
        work(tmp);//先判断一遍是否可以不用调换就可以达到目的图
        if(flag){
            printf("0
");
        }else{
            printf("%I64d
",bfs());
        }
    }
    return 0;
}