判断分析

判别分析

回忆一下，我们已经学过了聚类分析（物以类聚，人以群分），主成分分析（因子的线性变换），因子分析（因子内部的联系）。今天要介绍的又是另外一种多元分析，判别分析，他是对于给定的样本 ​ ，要判断他是来自哪一个总体。神奇不！！！

如何进行判别呢，主要有三种方法：

• 距离判别

• ​ 判别

• ​ 判别

其实总体的思路还是类似的，都是用一个标准来评价，这个样本更接近于哪一个总体，只不过三种方法的标准是不同的，这里我就只研究其中的 ​ 判别啦。其实 ​ 判别只需要稍微转换一下就是 ​ 判别了。

P266

clc,clear;
a = [24.8 24.1 26.6 23.5 25.5 27.4
    -2.0 -2.4 -3.0 -1.9 -2.1 -3.1]';
b = [22.1 21.6 22.0 22.8 22.7 21.5 22.1 21.4
    -0.7 -1.4 -0.8 -1.6 -1.5 -1.0 -1.2 -1.3]';
n1 = 6;
n2 = 8;
% 两个总体样本的均值向量
mu1 = mean(a);
mu2 = mean(b);
% 两个总体样本的协方差矩阵
sig1 = cov(a);
sig2 = cov(b);
​
% 两总体公共协方差矩阵的估计
sig = ((n1-1)*sig1+(n2-1)*sig2)/(n1+n2-2);
​
syms x1 x2;
x = [x1,x2];
​
% 构造判别函数
wx = (x-0.5*(mu1+mu2))*inv(sig)*(mu1-mu2)';
​
wx = vpa(wx,6);
ahat = subs(wx,{x1,x2},{a(:,1),a(:,2)});
bhat = subs(wx,{x1,x2},{b(:,1),b(:,2)});
​
ahat = vpa(ahat,6);
bhat = vpa(bhat,6);
beta = log(8/6);
sol1 = (ahat>beta);
sol2 = (bhat<beta);

 我们学过协方差和相关系数：

 

 

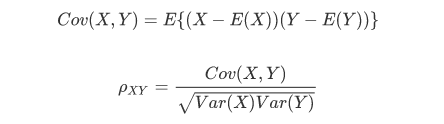
什么是协方差矩阵呢？

 

对于 ​Bayes 判别，他的判别函数是：

 

注意的是：这里的 ​u 是样本均值，要是总体均值那这个公式就变成了 ​Fisher 判别了，​sigma 是协方差矩阵。

求出判别函数：

 

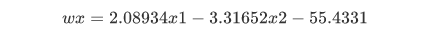
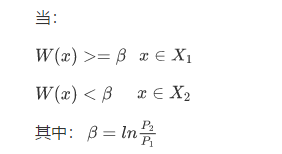
sol1 =
    0.28768207245178084585646161031036 < 3.0156097586564328594249673187733
    0.28768207245178084585646161031036 < 2.8796766343971853530092630535364
    0.28768207245178084585646161031036 < 10.092942700412879730720305815339
 0.28768207245178084585646161031036 < -0.032187096841215634412947110831738
    0.28768207245178084585646161031036 < 4.8098011348744364568119635805488
    0.28768207245178084585646161031036 < 12.096068323177490810849121771753
sol2 =
   -6.93708635319473501112952362746 < 0.28768207245178084585646161031036
 -5.6601960331855138974788133054972 < 0.28768207245178084585646161031036
 -6.8143689493495912756770849227905 < 0.28768207245178084585646161031036
 -2.4896817738427216681884601712227 < 0.28768207245178084585646161031036
 -3.0302676707810803691245382651687 < 0.28768207245178084585646161031036
 -7.1957368812991262529976665973663 < 0.28768207245178084585646161031036
 -5.2788281012359789201582316309214 < 0.28768207245178084585646161031036
 -6.4097161766704800811567110940814 < 0.28768207245178084585646161031036

还是可以看出，有一个判断错了。