ACM-ICPC (10/12)

01分数规划

背景：根据楼教主回忆，曾经在一场比赛中秒掉了一道最优比例生成树问题，导致很多人跟风失败，最终悲剧。

• 什么是01分数规划呢？

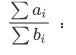这样的等式求最大，最小即为01分数规划。 　

如果你不知道该如何去解，你可能会去贪心，DP去做，但是这样是很复杂的。

• 解法：二分，迭代（计算几何大佬都知道这种方案，但是我不是）

• 直接二分ans，​ ​ ​ 根据符号二分转移。

例题一：pku 2796

 

题意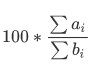： 最大。

#include <stdio.h>
#include <algorithm>
​
using namespace std;
​
const int maxn = 1005;
​
int n,k;
double a[maxn],b[maxn];
double c[maxn];
​
bool cmp(double a,double b) {
    return a > b;
}
​
bool calc(double x) {
    for(int i = 0; i < n; i++)
        c[i] = a[i] - x*b[i];
    sort(c,c+n,cmp);
​
    double sum = 0;
    for(int i = 0; i < n-k; i++)
        sum +=c[i];
    if(sum>=0) return true;
    return false;
​
}
​
int main()
{
    //freopen("in.txt","r",stdin);
    while(scanf("%d%d",&n,&k),n) {
​
        for(int i = 0; i < n; i++) scanf("%lf",&a[i]);
        for(int i = 0; i < n; i++) scanf("%lf",&b[i]);
​
        double l = 0,r = 1;
​
        while(r-l>1e-6) {
            double mid = (l + r)/2;
​
            if(calc(mid))
                l = mid;
            else r = mid;
​
        }
        printf("%.0lf
",l*100);
​
    }
    return 0;
}

例题二：pku 2728 最优比例生成树

题意：给定n 个点，坐标(x,y,z)，n条无向边的图，国王将这n个点连起来（生成树），建一条边有花费， 求单位最小花费最小比例。

同理：二分这个比例，边权为 ，最小生成树 ans >= 0，说明 x过小，二分转移 l = mid；

#include <stdio.h>
#include <string.h>
#include <math.h>
#include <vector>
#include <queue>
#include <map>
#include <set>
#include <iostream>
#include <algorithm>
​
using namespace std;
​
const int maxn = 1005;
​
double maps[maxn][maxn];
bool vis[maxn];
double dis[maxn];
​
int n;
​
double Prim() {
    memset(vis,false,sizeof(vis));
    for(int i = 1; i<= n; i++)
        dis[i] = 1000000000;
​
    double ans = 0;
    dis[1] = 0;
​
    for(int i = 1; i <= n; i++) {
        double tmp = 1000000000;
        int k = 0;
​
        for(int j = 1; j <= n; j++) {
            if(!vis[j]&&dis[j]<tmp) {
                tmp = dis[j];
                k = j;
            }
        }
​
        vis[k] = true;
        ans += tmp;
​
        for(int j = 1; j<= n; j++) {
            if(!vis[j]&&dis[j]>maps[k][j])
                dis[j] = maps[k][j];
        }
​
    }
    return ans;
}
​
struct Node {
    double x,y,z;
}nodes[maxn];
​
double dist(int i,int j,double x) {
    double fx = fabs(nodes[i].x-nodes[j].x);
    double fy = fabs(nodes[i].y-nodes[j].y);
    double fz = fabs(nodes[i].z-nodes[j].z);
    return fz - x*sqrt(fx*fx+fy*fy);
}
​
double eps = 1e-4;
​
int main()
{
    //freopen("in.txt","r",stdin);
    while(scanf("%d",&n),n) {
​
        for(int i = 1; i <= n; i++) scanf("%lf%lf%lf",&nodes[i].x,&nodes[i].y,&nodes[i].z);
​
        double l = 0,r = 1000000000;
​
        while(r-l>1e-5) {
            double mid = (r+l)/2;
​
            for(int i = 1; i <= n; i++)
                for(int j = 1; j <= n; j++)
                    maps[i][j] = dist(i,j,mid);
​
            double ans = Prim();
​
            if(ans<=0)
                r = mid;
            else l = mid;
        }
​
        printf("%.3f
",l);
    }
​
    return 0;
}

例题三：pku 3621 最优比例环。（双倍经验题Uva 11090，题意相反）

题意：给定一个L个节点，P条有向边的图，奶牛从一个城市出发，走一个环回到起点，点上有权值，边上也有长度，求单位长度的点权最大。

分析：还是二分 ans，由于是一个环，一条边上，算起点权值就好了。改边权， ，

由于求的是比例最大，这时SPFA，应反向松弛，才能得到最大的比例。

#include <stdio.h>
#include <string.h>
#include <math.h>
#include <string.h>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <string>
#include <iostream>
#include <algorithm>
​
using namespace std;
​
const int maxn = 1005;
​
struct Edge {
    int from,to;
    double dist;
};
​
struct BellmanFord
{
    int n, m;
    vector<Edge> edges;
    vector<int> G[maxn];
    bool inq[maxn];
    double d[maxn];
    int p[maxn];
    int cnt[maxn];
​
    void init(int n)
    {
        this->n = n;
        for(int i = 0; i < n; i++) G[i].clear();
        edges.clear();
    }
​
    void AddEdge(int from, int to, double dist)
    {
        edges.push_back((Edge)
        {
            from, to, dist
        });
        m = edges.size();
        G[from].push_back(m-1);
    }
​
    bool negativeCycle()
    {
        queue<int> Q;
        memset(inq, 0, sizeof(inq));
        memset(cnt, 0, sizeof(cnt));
        for(int i = 0; i < n; i++)
        {
            d[i] = 0;
            inq[0] = true;
            Q.push(i);
        }
​
        while(!Q.empty())
        {
            int u = Q.front();
            Q.pop();
            inq[u] = false;
            for(int i = 0; i < (int)G[u].size(); i++)
            {
                Edge& e = edges[G[u][i]];
                if(d[e.to] < d[u] + e.dist) //反向松弛
                {
                    d[e.to] = d[u] + e.dist;
                    p[e.to] = G[u][i];
                    if(!inq[e.to])
                    {
                        Q.push(e.to);
                        inq[e.to] = true;
                        if(++cnt[e.to] > n) return true;
                    }
                }
            }
        }
        return false;
    }
}sol;
int L,P;
double f[maxn];
double t[maxn];
​
vector<Edge> edgestmp;
​
int main()
{
    //freopen("in.txt","r",stdin);
    scanf("%d%d",&L,&P);
​
    sol.init(L);
    for(int i = 0; i < L; i++) scanf("%lf",&f[i]);
    for(int i = 0; i < P; i++) {
        int u,v;
        double dist;
        scanf("%d%d%lf",&u,&v,&dist);
        u--;v--;
        edgestmp.push_back((Edge){u,v,dist});
        sol.AddEdge(u,v,dist);
    }
​
    double l = 0,r = 10000;
    while(r-l>1e-4) {
        double mid = (r+l)/2;
​
        sol.init(L);
​
        for(int i = 0; i < P; i++) {
            int u = edgestmp[i].from;
            int v = edgestmp[i].to;
            double dist = edgestmp[i].dist;
            sol.AddEdge(u,v,f[u]-mid*dist);
        }
​
        if(sol.negativeCycle())
            l = mid;
        else r = mid;
    }
​
    printf("%.2f
",l);
    return 0;
}