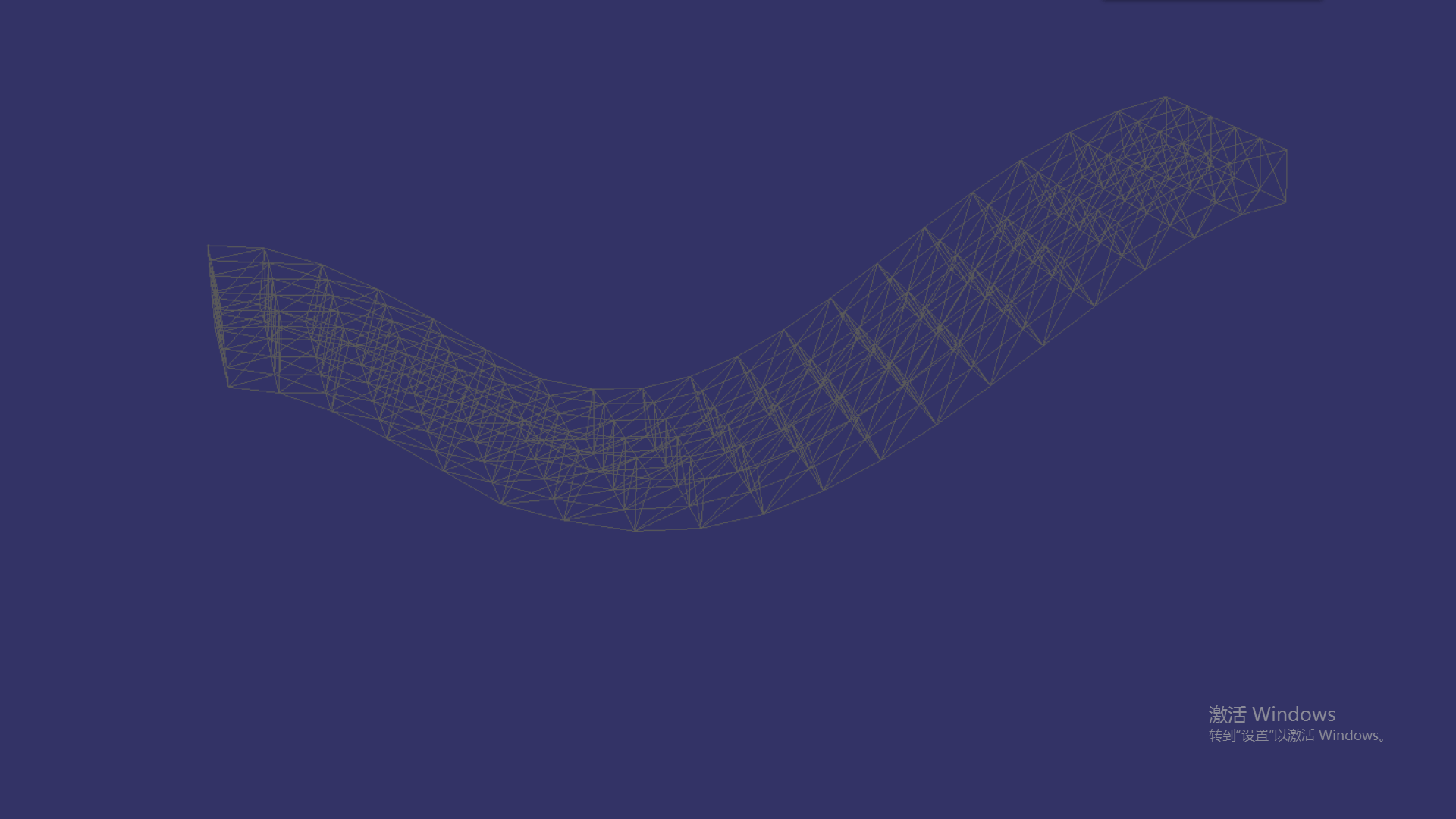
Green应变:
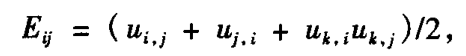
括号中最后一项为高阶小项,在非线性变形中起到主导作用,但是相应的形成了非线性方程组,求解计算量很大,非拧转情况下,可以忽略不计
本篇采用四面体单元结构(比如:一个正方体可以拆分为6个四面体),单元内任意一点的位移,可以转为四个顶点的位移插值:
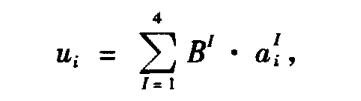
其中, a为顶点位移张量, B 为顶点已知的线性形状函数。由上式可以得到 位移梯度 与 顶点位移 的关系如下:
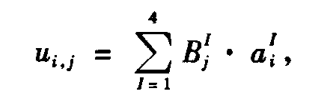
单元的刚度矩阵为:
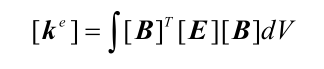
其中 B为形状函数矩阵(已知),V为四面体的体积, E 为材料的弹性矩阵:
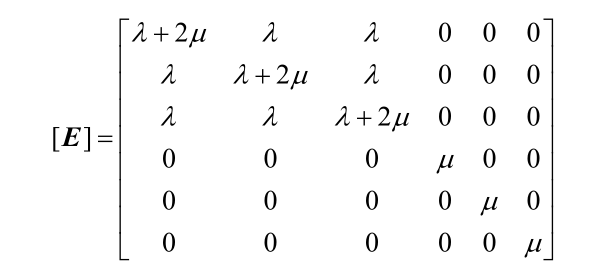
λ 和 µ 是为拉梅常数:

最后组装所有的单元刚度矩阵,成为全局刚度矩阵形式,是为一个线性方程组:
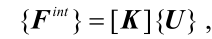
因为可以固定 约束顶点 或者 固定 力 的大小,使得方程不成为方阵,所以在程序里必须设计自动化方阵函数,使其成为方阵,最后使用共轭梯度法,可以提高求解方程的速度
简易效果: